
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Потенциальный напор.
В гидравлике слово напор применяется в особом смысле: напором принято называть удельную энергию жидкости, т. е. меру энергии, принадлежащей единице веса жидкости,
В соответствии с этим потенциальный напор будет представлять собой величину Н; при этом величина z(отметка точки) может быть названа геометрическим напором; величина же hизб (пьезометрическая высота) — напором давления. Достаточно величины Н, z, hизб умножить на единицу веса жидкости, и мы при этом получим соответствующие энергии этой единицы веса жидкости.
Можно сказать, что потенциальный напор (удельная потенциальная энергия) слагается из двух напоров: геометрического напора (удельной энергии положения) и напора давления (удельной энергии давления).
Все поясненные выше напоры имеют размерность длины и выражаются соответствующими отрезками: Н, z, hизб (рис. 2-9).
Следует запомнить, что с геометрической точки зрения потенциальный напор Н в данной точке (например, в точке n) по отношению к какой-либо горизонтальной плоскости сравнения 00 представляет собой сумму двух линейных величин: отметки данной точка z и соответствующей ей пьезометрической высоты hизб:
H = z + hизб или H = z +  [64]
[64]
Величина Н характеризуется следующей особенностью: для всех точек покоящейся жидкости величина Н одинакова: Н=const (по всему объему).
Для доказательства справедливости этого положения напишем:
H = z +  = z +
= z + 
 z +
z + 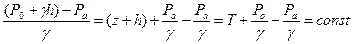 [65]
[65]
где T превышение горизонта жидкости в сосуде над плоскостью 00 (Т = const).
Возьмем закрытый сосуд (рис. 11). Наметим в жидкости ряд точек: 1, 2, 3, ... К каждой такой точке приключим пьезометр П. Основываясь на том, что Н=const (по всему объему) можем утверждать, что горизонт жидкости во всех пьезометрах должен установиться на одной и той же высоте,
Отсюда ясно, что по горизонтам жидкости в пьезометрах П можно провести некоторую плоскость РР, которая должна быть горизонтальной.
Эта горизонтальная плоскость РР называется пьезометрической плоскостью. Как видно, эта плоскость РР (или, как обычно говорят, пьезометрическая линия РР) возвышается над плоскостью сравнения на величину Н.
В заключение подчеркнем следующее: так как Н постоянна для всех точек покоящейся жидкости, то, следовательно, во всех точках такой жидкости удельная потенциальная энергия (ПЭ)уд одинакова.
(ПЭ)уд = const (по всему объему). [66]

|

|
Рис. 12
СООБЩАЮЩИЕСЯ СОСУДЫ
Предположим (рис. 13), что имеются два сообщающихся сосуда А и В, заполненных различными жидкостями плотности ρ1 и ρ2. Будем считать, что в общем случае сосуды закрыты и давления на свободных поверхностях жидкости в них соответственно равны Р1 и Р2.
Пусть поверхностью раздела жидкостей является поверхность аb в сосуде А и слой жидкости в этом сосуде равен h1. Определим положение уровня жидкости в сосуде В.

|
Гидростатическое давление в плоскости аb, в соответствии с уравнением Р = Р1 + ρgh [67]
будет Р = Р1 + ρ1gh1
если определять его исходя из известного давления P1 на поверхности жидкости в сосуде А.
Это давление можно также определить следующим образом:
Р = Р2 + ρ2gh2
| Рис. 13 |
где h2. — искомая глубина погружения поверхности аb под уровнем жидкости в сосуде В. Отсюда получаем условие для определения величины h2 Р1 + ρ1gh1 = Р2 + ρ2gh2
В частном случае, когда сосуды открыты (давления на свободных поверхностях равны атмосферному давлению) и, следо-
вательно, P1 = Р2 = Ратм
откуда ρ1h1 = ρ2h2 ;
ρ1/ρ2 = h2/h1 [68]
т. е, в сообщающихся сосудах при одинаковом давлении на свободных поверхностях высоты жидкостей, отсчитываемые от поверхности раздела, обратно пропорциональны плотностям жидкостей.
 На принципе сообщающихся сосудов основано устройство весьма простого прибора для определения плотности жидкости, изображенного на рис. 14, состоящего из двух сообщающихся сосудов — вертикальных стеклянных трубок А и В, соединенных между собой изогнутым коленом С. Одна из вертикальных трубок заполняется исследуемой жидкостью, а другая.— жидкостью известной плотности ρ1 (например, водой), причем в таких количествах, чтобы уровни жидкостей в среднем колене С находились на одной и той же отметке прибора 0. Далее измеряют высоты стояния жидкостей в трубках над этой отметкой h1 и h2 и, имея в виду, что эти высоты обратно пропорциональны плотностям жидкостей легко находят
На принципе сообщающихся сосудов основано устройство весьма простого прибора для определения плотности жидкости, изображенного на рис. 14, состоящего из двух сообщающихся сосудов — вертикальных стеклянных трубок А и В, соединенных между собой изогнутым коленом С. Одна из вертикальных трубок заполняется исследуемой жидкостью, а другая.— жидкостью известной плотности ρ1 (например, водой), причем в таких количествах, чтобы уровни жидкостей в среднем колене С находились на одной и той же отметке прибора 0. Далее измеряют высоты стояния жидкостей в трубках над этой отметкой h1 и h2 и, имея в виду, что эти высоты обратно пропорциональны плотностям жидкостей легко находят
плотность исследуемой жидкости
ρ2 = ρ1h1/ h2
| Рис. 14 |
Если оба сообщающихся сосуда будут заполнены одной и
той же жидкостью, то ρ1 = ρ2 и h1 = h2, т. е. высоты стояния жидкости в этих сосудах будут одинаковы. На этом основано устройство водомерных стекол.
| Принцип сообщающихся сосудов лежит также в основе ряда других приборов. служащих для измерения давлени и имеющих весьма широкое применение на практике На этом основано устройство так называемых водомерных стекол. |
§ 10. ПРИБОРЫ ДЛЯ ИЗМЕРЕНИЯ ДАВЛЕНИЙ
Для измерения гидростатического давления применяются различные приборы, которые можно подразделить на две основные группы — жидкостные и механические. Простейшим представителем приборов жидкостного типа является пьезометр, измеряющий давление в жидкости высотой столба той же жидкости.

|
Пьезометр представляет собой стеклянную трубку небольшого диаметра (обычно не менее 5 мм), открытую с одного конца и вторым концом присоединяемую к сосуду, в котором измеряется давление; схема пьезометра изображена на рис. 15.
Пусть давление р на поверхности жидкости в сосуде будет больше атмосферного. Тогда жидкость в трубке пьезометра поднимется выше уровня жидкости в сосуде на некоторую высоту hп. Гидростатическое давление жидкости в точке А, взятой
у основания пьезометрической трубки на глубине h, от свободной поверхности жидкости в сосуде, определяется по основному уравнению гидростатики [66]: PA = Pатм + ρg(hп +h)
следовательно hп + h = PA – Pатм/ρg, pA = P +ρgh
| Рис. 15. |
Таким образом, находим P = Pатм +ρghп
Отсюда видно, что высота поднятия жидкости в пьезометрической трубке, так называемая пьезометрическая высота, характеризует избыточное давление в сосуде и может служить мерой для определения его значения.
Измерение давления высотой столба жидкости весьма удобно и часто применяется в технике. Полезно запомнить, что давление, равное 1 кгс/см2 (техническая атмосфера), соответствует весу столба воды с основанием 1 см2 высотой
hпв = Р/ ρвg = Р/γв = 1/0,001 = 1000см = 10м
или весу столба ртути с тем же основанием 1 см2 высотой 735 мм.
hп.рт = Р/ρртg = P/γрт = 1/0,0136 = 73,5 см = 735 мм.
Физическая же атмосфера (1,033 кгс/см2) определяется ртутным столбом в 760 мм. Поэтому, например, если давление в сосуде будет 2,5 ат, или, что то же самое, 2,5 кгс/см2, его можно будет определить так же, как давление, равное 25 м водяного или 183,75 см ртутного столба.
Для нефтей и нефтепродуктов, имеющих меньшие плотности, высота соответствующих столбов жидкости в пьезометре при тех же давлениях, естественно, будет больше.
Пьезометр — очень чувствительный и точный прибор, однако он удобен только для измерения небольших давлений (не свыше 0,5 ати); при больших давлениях трубка пьезометра получается чрезмерно длинной, что осложняет измерения. В этих случаях применяют так называемые жидкостные манометры, в которых давление уравновешивается не жидкостью, находящейся в сосуде, как это имеет место в пьезометре, а жидкостью большей плотности. Обычно такой жидкостью является ртуть. Так как плотность ртути больше плотности воды в 13,6 раза, то при измерении одних и тех же давлений трубка ртутного манометра оказывается значительно короче пьезометрической трубки и сам прибор получается более компактным.
Ртутный манометр(рис. 16) представляет собой обычно U-образную стеклянную трубку, изогнутое колено которой заполняется ртутью. Под действием давления р в сосуде уровень
в левом колене манометра понижается, а в правом — повышается. При этом гидростатическое давление в точке А, взятой на поверхности ртути в левом колене, по аналогий с предыдущим, определяется следующим образом:
PA = P + ρ1gh1 = Pатм + ρртghрт ; где ρ1 и ρрт плотности соответственно жидкости и ртути в сосуде
Отсюда: P = Pатм + ρртghрт - ρ1gh1;

|
|

Рис. 16. Рис. 17 Рис. 18
В тех случаях, когда необходимо измерить не давление в сосуде, а разность давлений в двух сосудах или же в двух точках жидкости в одном и том же сосуде, применяют дифференциальные манометры.
Дифференциальный манометр, присоединенный к двум сосудам А и В, представлен на рис. 17. Здесь, так же как и раньше, для давления р на уровне поверхности ртути в левом колене (точка С) имеем
P = PA + ρ1gh1 = PВ+ ρ2gh2 + ρртgh
откуда PA - PB = ρ1g(h2 – h1) + ρртgh
или, так как h2 – h1 =-h то PA - PB = (ρрт - ρ1)gh
Таким образом, разность давлений определяется разностью уровней в двух коленах дифференциального манометра.
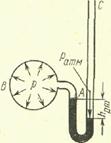
Вакуумметром Для измерения давления меньше атмосферного (в сосуде имеется вакуум) служат приборы, называемые вакуумметрами. Однако вакуумметры обычно измеряют не непосредственно давление, а вакуум, т. е. недостаток давления до атмосферного. Принципиально они ничем не отличаются от ртутных манометров и представляют собой заполненную ртутью изогнутую трубку (рис. 18), один конец которой А соединяется с сосудом В, где измеряется давление р, а другой конец С открыт. Например, нужно измерить давление газа в сосуде В. В этом случае имеем
Р = Р + ρрт ghрт
откуда
Р = Ратм — ρрт ghрт
Высоту 
соответствующую вакууму в сосуде (рвак = ратм -р), обычно называют вакуумметрической высотой и обозначают hвак Отсюда следует, что величину вакуума также можно измерять высотой столба жидкости. Так, если показание ртутного вакуумметра hрт = 50 см, то вакуум
Рвак = ρрт ghрт = γртhрт = 0,0136.50 = 0,68 кгс/см2.
Дата добавления: 2015-04-18; просмотров: 557; Мы поможем в написании вашей работы!; Нарушение авторских прав |