Коэффициент линейных потерь при ламинарном движении жидкости

Зная закон распределения скорости в поперечном сечении, можно вывести теоретические формулы для определения расхода жидкости, потери напора на трение, а также коэффициент линейных потерь l при ламинарном режиме течения.

Средняя по сечению скорость согласно формуле (6.8) равна

.

Учитывая, что и 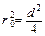, получим

.

Отсюда

или

.

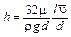После некоторых преобразований найдём

.

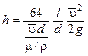Отсюда получим

.

Сравнивая с формулой Дарси - Вейсбаха

,

находим

.

Последнее соотношение представляет формулу Пуазейля для определения коэффициента трения l (коэффициента линейных потерь).

Логарифмируя формулу Пуазейля, получим

.

Из последнего соотношения следует, что зависимость l от Re будет выражаться в логарифмических координатах прямой линией с углом наклона к оси абсцисс, равным 45⁰ (рис. 6.9).

Многочисленные эксперименты полностью подтверждают правильность для ламинарного изотермического потока полученных теоретических выводов. Тем самым подтверждается и правильность закона Ньютона для внутреннего трения, положенного в основу этих выводов. При Re ³ 2300, т.е. при турбулентном режиме, закон Пуазейля неприменим.