Ламинарное движение жидкости

Определим основные закономерности ламинарного потока при равномерном движении в круглых трубах. При этом будем рассматривать участок стабилизированного течения, т.е. участок, на котором профиль скорости ламинарного потока полностью сформировался (см. §6.7).

Ранее (см. § 6.1) было показано, что ламинарное течение имеет слоистый характер без перемешивания частиц. При этом имеют место только направления потока, параллельные оси трубы при полном отсутствии поперечных движений жидкости. Скорость в слое, непосредственно соприкасающемся со стенками, вследствие прилипания жидкости к стенке (из-за вязкости жидкости) равна нулю. Максимального значения скорость достигает в слое, движущемся по оси трубы.

Для принятой схемы движения необходимо установить закон распределения скоростей в поперечном сечении потока, получить расчетные зависимости для определения расхода жидкости и потерь напора на трение по длине потока.

Рассмотрим ламинарный равномерный поток жидкости в трубе круглого сечения (рис. 6.6).

Рис. 6.6

Основное уравнение равномерного потока имеет вид

. (6.3)

По закону Ньютона для внутреннего трения

. (6.4)

В трубе круглого сечения гидравлический радиус отсека потока с геометрическим радиусом r равен . Поскольку при ламинарном режиме течения жидкости в трубе векторы скорости симметричны относительно продольной оси, то за нормаль следует принять радиус отсека потока.

Тогда

.

Знак минус взят потому, что при увеличении радиуса скорость убывает.

Уравнения (6.3) и (6.4) примут вид

; .

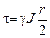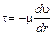Приравнивая правые части этих уравнений, находим

или

.

Интегрируя, получим (учитывая, что в равномерном потоке , т.е. не зависит от r)

.

Постоянная интегрирования C находится из граничных условий. При (скорость движения жидкости на стенке равна 0). Тогда

.

Отсюда

. (6.5)

Из полученного уравнения видно, что скорость в поперечном сечении потока изменяется по закону параболы (рис. 6.7).

Максимальная скорость имеет место на оси трубы при . Тогда из последнего уравнения следует

.

Или, преобразуя уравнение (6.5)

и, учитывая формулу для u _max, получим

,

т.е. распределение безразмерных скоростей является лишь функцией безразмерной величины . Эта функция одинакова во всех случаях ламинарного движения любой жидкости внутри круглых труб. Следовательно, все рассматриваемые течения подобны независимо от числа Re. Такие явления называют автомодельными.

Полученную выше формулу для касательных напряжений

,

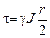учитывая, что , можно записать в виде

,

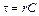где .

Рис.6.7

Отсюда формула для t принимает вид

.

Из этой формулы следует, что касательное напряжение является линейной функцией текущего радиуса трубы r. Максимального значения t принимает на стенке трубы, минимального ( ) - в ее центре. Эпюра касательного напряжения представлена на рис.6.7.