Физический смысл критериев подобия

Процесс течения реальной жидкости описывается сложной системой дифференциальных уравнений (система уравнений Навье-Стокса) и условиями однозначности с большим числом переменных величин. Попытки аналитического решения этой системы уравнений представляют серьезные трудности. Поэтому большое значение приобретают экспериментальные исследования. С помощью эксперимента для отдельных значений аргумента можно получить численные значения искомых переменных, а затем подобрать уравнения, описывающие результаты опытов. Однако при изучении столь сложного явления как течение реальной жидкости не всегда легко проводить и опытное исследование. Кроме того, здесь нужно быть уверенным, что результаты, получаемые с помощью какой-либо установки (модели), можно перенести и на другие, аналогичные процессы (образец). Для решения этих трудностей и предназначена теория подобия.

На основе теории подобия размерные физические величины объединяются в безразмерные комплексы. При этом число таких комплексов оказывается существенно меньшим числа величин, из которых они составлены. Полученные безразмерные комплексы рассматриваются как новые переменные.

Кроме того, теория подобия устанавливает условия, при которых результаты экспериментальных исследований можно распространить и на другие явления, подобные исследуемому.

В уравнениях и условиях однозначности различают три вида величин (применительно к системе дифференциальных уравнений Навье-Стокса).

1. Независимые переменные. К ним относятся координаты x, y, z и время t.

2. Зависимые переменные (искомые функции), которые однозначно определяются значениями независимых переменных. К их числу относится давление р и составляющие скорости u_x, u_y, u_z по координатным осям.

3. Постоянные величины (константы), которые для определенной задачи являются постоянными величинами, не зависящими от других переменных. Однако при переходе к другим задачам они могут изменяться. Постоянными величинами являются линейные размеры, вязкость, плотность и др.

После перевода математической постановки задачи к безразмерному виду получаем комплекс критериев подобия.

Критериям подобия присвоены имена ученых, которые внесли значительный вклад в развитие гидродинамики.

Первый из этих безразмерных комплексов обозначают

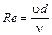
и называют критерием Рейнольдса. Он характеризует отношение сил инерции и сил вязкости. При заданных диаметре трубопровода d и вязкости жидкости n критерий Рейнольдса зависит лишь от скорости течения v и поэтому является, по сути дела, безразмерной скоростью.

Безразмерный комплекс

называется критерием Эйлера. Он характеризует отношение сил давления и сил инерции. Для несжимаемой жидкости с постоянными физическими параметрами большой интерес представляет не абсолютное давление p, а его изменение. Поэтому критерий Eu обычно записывают в виде

,

где p₀ – фиксированное значение давления (например на входе в канал).

Безразмерный комплекс

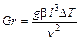
называют критерием Грасгофа. Здесь g – ускорение силы тяжести; - коэффициент объемного расширения (1/К); n- кинематический коэффициент вязкости; l – определяющий размер; DТ – изменение температуры в процессе; r - плотность.

Критерий Грасгофа характеризует подъемную силу, возникающую в жидкости вследствие разности плотности из-за изменения температуры.

В случае, когда разность плотностей обусловлена не температурным фактором, а составом жидкости (присутствие примесей или других жидкостей, удельный вес которых отличается от удельного веса основной жидкости), критерием подобия будет диффузионное число Архимеда

,

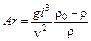где r₀ и r - плотность одной и другой фаз.

В случае, когда в жидкости велики силы поверхностного натяжения, вводится критерий подобия Вебера

,

где s - коэффициент поверхностного натяжения.

Критерий подобия Вебера представляет собой отношение сил инерции к силам поверхностного натяжения.

Критерий подобия Фруда

есть мера отношения потенциальной энергии массовых сил к силам инерции потока.

При исследовании неустановившихся явлений используются критерии подобия Струхаля

и Фурье

,

где t – время; а – коэффициент температуропроводности, м²/с.

Критерий подобия Струхаля характеризует составляющие инерционных сил, зависящих от времени.

Критерий подобия Фурье представляет безразмерное время.

При исследовании процессов теплопередачи и диффузии используют критерий подобия Пекле

,

характеризующий отношение тепла, переносимого конвекцией, к теплу, передаваемому теплопроводностью. Например, при больших числах Ре преобладающим будет конвективный теплоперенос и наоборот.

Критерий подобия Прандтля

полностью составлен из физических параметров, а потому и он является физическим параметром. Этот критерий имеет смысл подобия полей температур и скоростей.