УРАВНЕНИЕ БЕРНУЛЛИ ДЛЯ ЭЛЕМЕНТАРНОЙ СТРУЙКИ ИДЕАЛЬНОЙ ЖИДКОСТИ. В технической гидромеханике уравнение Бернулли устанавливает зависимость между скоростью и давлением в различных сечениях одной и той же элементарной

В технической гидромеханике уравнение Бернулли устанавливает зависимость между скоростью и давлением в различных сечениях одной и той же элементарной струйки.

При выводе этого уравнения принимаются следующие допущения.

1. Движение жидкости установившееся.

2. Массовые силы имеют потенциал, т.е.

;

;

.

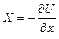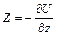3. Жидкость баротропна, т.е. плотность является функцией лишь одного давления .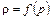

Запишем уравнения движения Эйлера

;

;

.

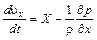Умножим обе части каждого из уравнений на dx, dy , dz соответственно и сложим полученные соотношения

(4.11)

Считая dx, dy, dz не любыми произвольными приращениями координат, а приращениями, взятыми по какой-либо линии тока, а также учитывая, что при установившемся движении линии тока и траектории частиц совпадают, получим

Преобразуем левую часть уравнения (4.11)

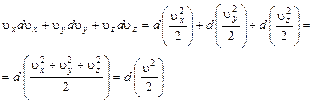
В правой части уравнения будем иметь

.

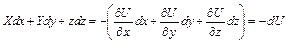Так как , то .

Отсюда уравнение (4.11) примет вид

Или

.

Интегрируя последнее соотношение по линии тока, получим

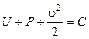, (4.12)

где 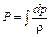- функция Громеко; С – константа интегрирования.

Соотношение (4.12) называется интегралом Бернулли или уравнением Бернулли в общем виде. Оно показывает, что при установившемся движении баротропной идеальной жидкости в поле потенциальных сил сумма трех членов U, P и одинакова во всех точках на данной линии тока. Очевидно, что оно будет верно также и для элементарной струйки тока, выделенной вокруг данной линии тока.

В частном случае тяжелой несжимаемой невязкой жидкости будем иметь потенциал массовой силы тяжести в виде

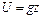. (4.13)

Для несжимаемой жидкости и функция Громеко приводится к виду

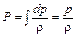. (4.14)

Подставляя (4.13), (4.14) в (4.12), получим

.

С учетом найдем

.

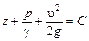Отсюда для двух различных точек линии тока или для двух различных сечений элементарной струйки можно написать

.

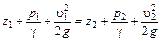Таким образом, для всех частиц, расположенных на одной и той же линии тока, сумма трех величин 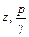и сохраняет постоянное значение.