Условия плавучести и остойчивости тел, частично погруженных в жидкость

Наличие условия необходимо для равновесия тела, погруженного в жидкость, но еще недостаточно. Для равновесия тела, кроме равенства , необходимо также, чтобы линии этих сил были направлены по одной прямой, т.е. совпадали (рис. 3.25 а).

Рис. 3.25

Если тело однородно, то точки приложения указанных сил всегда совпадают и направлены по одной прямой. Если тело неоднородно, то точки приложения этих сил не совпадут и силы G и F_z образуют пару сил (см. рис. 3.25 б, в). Под действием этой пары сил тело будет вращаться в жидкости до тех пор, пока точки приложения сил G и F_z не окажутся на одной вертикали, т.е. момент пары сил будет равен нулю (рис.3.26).

Наибольший практический интерес представляет исследование условий равновесия тел, частично погруженных в жидкость, т.е. при плавании тел.

Способность плавающего тела, выведенного из состояния равновесия, вновь возвращаться в это состояние называется остойчивостью.

Рассмотрим условия, при которых плавающее на поверхности жидкости тело остойчиво.

На рис. 3.27 (а, б) C - центр тяжести (точка приложения равнодействующей сил веса G);
D - точка приложения равнодействующей выталкивающих сил F_z; M - метацентр (точка пересечения равнодействующей выталкивающих сил с осью плавания 00).

Дадим некоторые определения.

Вес жидкости, вытесненной погруженным в нее телом, называется водоизмещением.

Рис. 3.27

Точка приложения равнодействующей выталкивающих сил называется центром водоизмещения (точка D).

Расстояние MC между метацентром и центром водоизмещения называется метацентрическим радиусом.

Таким образом, плавающее тело имеет три характерные точки:

1. Центр тяжести C, не меняющий своего положения при крене.

2. Центр водоизмещения D, перемещающийся при крене тела, так как очертания объема, вытесняемого в жидкости, при этом меняются.

3. Метацентр M, также изменяющий свое положение при крене.

При плавании тела могут представиться следующие 3 основных случая в зависимости от относительного расположения центра тяжести C и метацентра M.

1. Случай остойчивого равновесия. В этом случае метацентр лежит выше центра тяжести (рис.3.27,а) и при крене пара сил G и F_z стремится возвратить тело в первоначальное состояние (тело вращается против часовой стрелки).

2. Случай безразличного равновесия. В этом случае метацентр и центр тяжести совпадают и тело, выведенное из состояния равновесия, остается неподвижным.

3. Случай неостойчивого равновесия. Здесь метацентр лежит ниже центра тяжести (рис. 3.27,б) и образовавшаяся при крене пара сил вызывает вращение тела по часовой стрелке, что может привести к опрокидыванию плавающего средства.

Задачи

Задача 1. Паровой прямодействующий насос подает жидкость Ж на высоту Н (рис. 3.28). Найти рабочее давление пара при следующих исходных данных: ; ; . Жидкость – вода ( ). Найти также силу, действующую на малый и большой поршни.

Рис. 3.28

Решение.Найдем давление на малом поршне

.

Сила , действующая на малый поршень, будет

.

Эта же сила действует на большой поршень, т.е.

.

Отсюда

.

Задача 2.Определить силу прессования , развиваемую гидравлическим прессом, у которого диаметр большого поршня 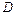, а малого – , при следующих исходных данных (рис. 3.29):

; ; ; ; .

Рис. 3.29

Решение. Найдем силу 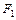, действующую на малый поршень. Для этого составим условие равновесия рычага пресса

.

Отсюда

Давление жидкости под малым поршнем будет

,

где .

Давление жидкости под большим поршнем

,

где .

По закону Паскаля давление в жидкости передается по всем направлениям без изменения. Отсюда 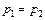или

.

Отсюда

.

Глава 4

Гидродинамика

Раздел гидравлики, в котором изучаются законы движения жидкости, называется гидродинамикой. При изучении движения жидкостей рассматриваются две основные задачи.

1. Заданы гидродинамические характеристики потока (скорость и давление); требуется определить силы, действующие на жидкость.

2. Заданы силы, действующие на жидкость; требуется определить гидродинамические характеристики потока.

Применительно к идеальной жидкости гидродинамическое давление имеет те же свойства и тот же смысл, что и гидростатическое давление. При анализе движения вязкой жидкости оказывается, что

,

где - действительные нормальные напряжения в рассматриваемой точке, относящиеся к трем произвольно намеченным в этой точке взаимно ортогональным площадкам. Гидродинамическим давлением в точке считают величину

.

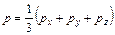При этом считается, что величина p не зависит от ориентировки взаимно ортогональных площадок.

В дальнейшем будет рассматриваться задача определения скорости и давления при известных силах, действующих на жидкость. Следует отметить, что скорость и давление для разных точек жидкости будут иметь различные величины и, кроме того, для данной точки пространства они могут изменяться во времени.

Для определения составляющих скорости по координатным осям , , и давления p в гидравлике рассматриваются следующие уравнения.

1. Уравнение несжимаемости и неразрывности движущейся жидкости (уравнение баланса расхода жидкости).

2. Дифференциальные уравнения движения (уравнения Эйлера).

3. Уравнение баланса удельной энергии потока (уравнение Бернулли).

Ниже будут приведены все эти уравнения, составляющие теоретическую базу гидродинамики, с предварительными пояснениями некоторых исходных положений из области кинематики жидкости.