Закон Архимеда. Закон Архимеда формулируется в виде следующего утверждения - на тело, погруженное в жидкость, действует выталкивающая сила

Закон Архимеда формулируется в виде следующего утверждения - на тело, погруженное в жидкость, действует выталкивающая сила, направленная вверх и равная весу вытесненной им жидкости. Эта сила называется поддерживающей. Она является равнодействующей сил давления, с которыми жидкость, находящаяся в покое, действует на покоящееся в нем тело.

Для доказательства закона выделим в теле элементарную вертикальную призму с основаниями dw_n1 и dw_n2 (рис. 3.23). Вертикальная проекция элементарной силы, действующей на верхнее основание призмы, будет

,

Рис. 3.23

где p₁ - давление на основании призмы dw_n1; n₁ - нормаль к поверхности dw_n1.

Так как

,

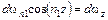где dw_z - площадь призмы в сечении, перпендикулярном оси z, то

.

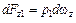Отсюда, учитывая, что по формуле гидростатического давления , получим

.

Аналогично вертикальная проекция элементарной силы, действующей на нижнее основание призмы, находится по формуле

.

Суммарная вертикальная элементарная сила, действующая на призму, будет

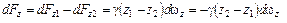
или

.

Интегрируя это выражение при 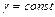, получим

,

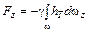где - объем тела, погруженного в жидкость, где h_T это высота погруженной части тела на данной вертикали.

Отсюда для выталкивающей силы F_z получим формулу

.

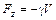Выделяя в теле элементарные горизонтальные призмы и производя аналогичные выкладки, получим , .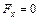

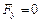Тогда

,

где G - вес жидкости, вытесненной телом. Таким образом, выталкивающая сила, действующая на тело, погруженное в жидкость, равна весу жидкости, вытесненной телом, что и требовалось доказать.

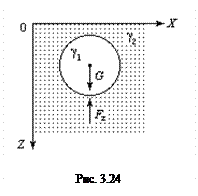
Из закона Архимеда следует, что на тело, погруженное в жидкость, в конечном счете действуют две силы (рис. 3.24).

1. Сила тяжести - вес тела .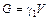

2. Поддерживающая (выталкивающая) сила 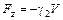, где g₁ - удельный вес тела; g₂ - удельный вес жидкости.

При этом могут иметь место следующие основные случаи:

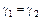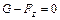1. Удельный вес тела и жидкости одинаковы . В этом случае , равнодействующая , и тело будет находиться в состоянии безразличного равновесия, т.е. будучи погружено на любую глубину, оно не будет ни всплывать, ни тонуть.

2. При g₁> g₂ , 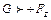. Равнодействующая направлена вниз, и тело будет тонуть.

3. При g₁< g₂ . Равнодействующая направлена вверх, и тело будет всплывать. Всплытие тела будет продолжаться до тех пор, пока выталкивающая сила не уменьшится настолько, что сделается равной силе веса, т.е. пока не будет 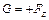. После этого тело будет плавать на поверхности.