
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
ОСНОВНЫЕ КИНЕМАТИЧЕСКИЕ ПОНЯТИЯ И ОПРЕДЕЛЕНИЯ. ДВА МЕТОДА ИССЛЕДОВАНИЯ ДВИЖЕНИЯ ЖИДКОСТИ
При изучении движения жидкости можно пользоваться двумя методами исследования. Первый метод, развитый Лагранжем и названный субстанциональным, заключается в том, что движение всей жидкости изучается путем исследования движения ее отдельных индивидуальных частиц.
Второй метод, развитый Эйлером и названный локальным, состоит в том, что движение всей жидкости изучается путем исследования движения в отдельных неподвижных точках, через которые протекает жидкость.
В гидродинамике применяются оба эти метода. Однако более распространен метод Эйлера, благодаря его простоте. По методу Лагранжа в начальный момент времени t0 отмечают в жидкости определенные частицы и далее следят во времени за движением каждой отмеченной частицы и за ее кинематическими характеристиками. Положение каждой частицы жидкости в момент времени t0 определяется тремя координатами в неподвижной системе координат, т.е. тремя уравнениями
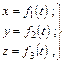 (4.1)
(4.1)
где х, у, z - координаты частицы; t - время.
Для составления уравнений, характеризующих движение различных частиц потока, необходимо учитывать положение частиц в начальный момент времени, т.е. начальные координаты частиц.
Например, точка М (рис. 4.1) в момент времени t = 0 имеет координаты а, b, с. Соотношения (4.1) с учетом а, b, с примут вид
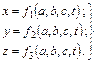 (4.2)
(4.2)
В соотношениях (4.2) начальные координаты а, b, с могут рассматриваться как независимые переменные (параметры). Следовательно, текущие координаты x, y, z некоторой движущейся частицы являются функциями переменных а, b, с, t, которые называются переменными Лагранжа.
При известных соотношениях (4.2) движение жидкости вполне определено. Действительно, проекции скорости на координатные оси определяются соотношениями (как первые производные от координат по времени)

 ;
;
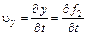 ; (4.3)
; (4.3)
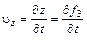 .
.
Проекции ускорений находятся как вторые производные от координат (первые производные от скорости) по времени (соотношения 4.5).
Траектория любой частицы определяется непосредственно из уравнений (4.1) путем нахождения координат x, y, z выбранной частицы жидкости для ряда моментов времени.
По методу Эйлера изучение движения жидкости состоит: а) в исследовании изменений во времени векторных и скалярных величин в некоторой фиксированной точке пространства; б) в исследовании изменений этих величин при переходе от одной точки пространства к другой.
Таким образом, в методе Эйлера предметом изучения являются поля тех или иных векторных или скалярных величин. Полем какой-либо величины, как известно, называется часть пространства, в каждой точке которого имеется определенное значение этой величины.
Математически поле, например скоростное, описывается следующими уравнениями
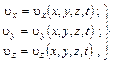 (4.4)
(4.4)
т.е. скорость
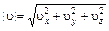
является функцией координат и времени.
Переменные x, y, z, t называются переменными Эйлера.
Таким образом, в методе Эйлера движение жидкости характеризуется построением поля скоростей, т.е. картины движения в различных точках пространства в каждый данный момент времени. При этом скорости во всех точках определяются в виде функций (4.4).
Метод Эйлера и метод Лагранжа математически связаны между собой. Например, в методе Эйлера, частично используя метод Лагранжа, можно следить за движением частицы не в течение времени t (как это следует по Лагранжу), а в продолжение элементарного отрезка времени dt , в течение которого данная частица жидкости проходит через рассматриваемую точку пространства. При этом для определения проекций скорости на координатные оси можно будет пользоваться соотношениями (4.3).
Из (4.2) следует, что координаты x, y, z являются функциями времени. Тогда 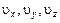 будут сложными функциями времени. По правилу дифференцирования сложных функций будем иметь
будут сложными функциями времени. По правилу дифференцирования сложных функций будем иметь

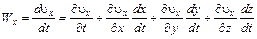 ;
;
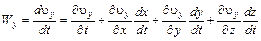 ; (4.5)
; (4.5)
 ,
,
где  – проекции ускорения движущейся частицы на соответствующие координатные оси.
– проекции ускорения движущейся частицы на соответствующие координатные оси.
Так как для движущейся частицы
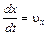 ,
,  ,
,  ,
,
то
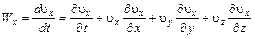 ;
;
 ;
;
 .
.
Частные производные
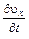 ,
, 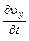 ,
, 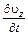
называются проекциями локального (местного) ускорения.
Суммы вида

называется проекциями конвективного ускорения.
Полные производные
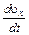 ,
,  ,
, 
называются еще субстанциональными или индивидуальными производными.
Локальное ускорение определяет изменение во времени скорости в данной точке пространства. Конвективное ускорение определяет изменение скорости по координатам, т.е. при переходе из одной точки пространства в другую.
§ 4.2. Траектории частиц и линии тока
Траекторией движущейся частицы жидкости называется путь одной и той же частицы, прослеженной во времени. Изучение траекторий частиц лежит в основе метода Лагранжа. При исследовании движения жидкости по методу Эйлера общее представление о движении жидкости можно составить при помощи построения линий тока (рис. 4.2, 4.3). Линией тока называется такая линия, в каждой точке которой в данный момент времени t векторы скорости являются касательными к этой линии.
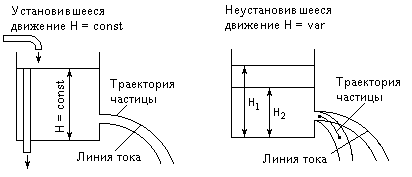
| Рис.4.2. | Рис.4.3. |
При установившемся движении (см. §4.3), когда уровень жидкости в емкости не изменяется (см. рис. 4.2), траектории частиц и линии тока совпадают. В случае неустановившегося движения (см. рис. 4.3) траектории частиц и линии тока не совпадают.
Следует подчеркнуть разницу между траекторией частицы и линией тока. Траектория относится лишь к одной определенной частице, изучаемой в течение определенного отрезка времени. Линия тока относится к определенной совокупности различных частиц, рассматриваемых в одно мгновение
(в данный момент времени).
Дата добавления: 2015-04-18; просмотров: 1032; Мы поможем в написании вашей работы!; Нарушение авторских прав |