Центр давления и определение его координат

Точка приложения суммарной силы давления называется центром давления. Определим координаты центра давления 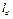и 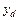(рис. 3.20). Как известно из теоретической механики, при равновесии момент равнодействующей F относительно некоторой оси равен сумме моментов составляющих сил dF относительно той же оси.

Составим уравнение моментов сил F и dF относительно оси 0y.

.

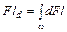Силы F и dF определим по формулам

;

.

Тогда

.

Cокращая выражение на g и sina, получим

,

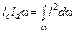где 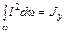- момент инерции площади фигуры относительно оси 0y.

Отсюда

.

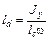Заменив по известной из теоретической механики формуле, где J_c - момент инерции площади фигуры относительно оси, параллельной 0y и проходящей через центр тяжести, получим

.

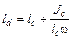Из этой формулы следует, что центр давления всегда расположен ниже центра тяжести фигуры на расстоянии . Это расстояние называется эксцентриситетом и обозначается буквой e.

Координата y_d находится из аналогичных соображений

,

где - центробежный момент инерции той же площади относительно осей y и l. Если фигура симметрична относительно оси, параллельной оси 0l (рис. 3.20), то, очевидно, , где y_c - координата центра тяжести фигуры.