ИНТЕГРИРОВАНИЕ УРАВНЕНИЙ ЭЙЛЕРА ДЛЯ СЛУЧАЯ ОТНОСИТЕЛЬНОГО ПОКОЯ ЖИДКОСТИ

Пусть жидкость находится в емкости, которая движется прямолинейно и равноускоренно по горизонтальной плоскости с ускорением а (рис. 3.13).

Масса жидкости при движении находится под действием массовой силы тяжести и силы инерции от горизонтального перемещения. Соответствующие проекции массовых сил будут равны .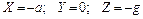

Уравнение (3.15), учитывая массовые силы, примет вид

.

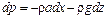Переменные в уравнении разделены. Интегрируя его, получим

, (3.26)

где C - постоянная интегрирования, определяемая из граничных условий, которые в данном случае имеют вид 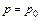при x=0 и z=0.

Отсюда

. (3.27)

Подставляя (3.27) в (3.26), найдем

. (3.28)

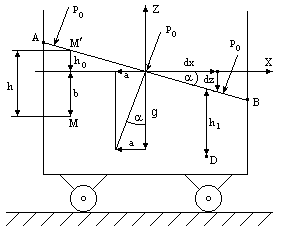
Рис. 3.13

Уравнение (3.28) для свободной поверхности, где p = p₀, примет вид

.

Отсюда

.(3.29)

Так как a/g является константой, то уравнение (3.29) будет уравнением прямой линии. Это означает, что плоскость, проведенная через оси x и z , будет пересекать наружную поверхность жидкости по линии AB.

Отношение a/g представляет тангенс угла наклона прямой AB к горизонтальной плоскости .

Отсюда .

Запишем уравнение (3.28) для некоторой точки M в виде

или

. (3.30)

Согласно (3.29) первый член в правой части уравнения (3.30) будет ,так как точка M¢ находится на поверхности.

Отсюда, учитывая, что , а получим

или

. (3.31)

Уравнение (3.31) представляет формулу гидростатического давления
(3.23). Таким образом, давление в любой точке жидкости, движущейся вместе с емкостью прямолинейно и равноускоренно, определяется по формуле гидростатического давления, где h - глубина погружения точки под поверхностью жидкости. Например, давление в точке D будет .

Рассмотрим теперь жидкость, находящуюся в цилиндрической емкости, которая вращается вокруг вертикальной оси с постоянной угловой скоростью w (рис. 3.14 ).

Центробежная сила на единицу массы

,

где V -окружная скорость.

Проекции массовых сил на соответствующие оси координат будут

;

;

.

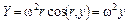Подставляя их значения в соотношение

,

получим

.

Интегрируя, найдем

,

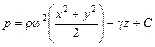где C - постоянная интегрирования. Так как при x = 0, y = 0, z = 0 p = p_0, то
C = p₀. Учитывая, что , находим

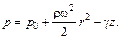(3.32)

По формуле (3.32) можно найти давление в любой точке М жидкости по глубине емкости. Для нахождения поверхностей равного давления положим dp=0, тогда будем иметь

.

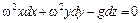Интегрируя, получим

.

Отсюда

.

Следовательно, поверхности равного давления представляют собой параболоиды вращения.

При r = 0, z = 0 получаем C = 0 для уравнения свободной поверхности. Тогда уравнение свободной поверхности

.

Найдем давление в некоторой точке М, расположенной на глубине h от поверхности. Обозначив аппликату свободной поверхности через z₀ (точка М), получим

.

Подставляя это выражение в (3.32), находим

или

,

где . Таким образом, вновь получили формулу гидростатического давления.