ОСНОВНОЕ УРАВНЕНИЕ ГИДРОСТАТИКИ

Рассмотрим наиболее часто встречающийся случай, когда покоящаяся жидкость заключена в сосуде и находится под воздействием только силы тяжести (рис. 3.7).

Рис. 3.7

В выражении

; ; .

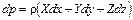
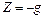Тогда

или

.

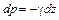Интегрируя, получим

. (3.21)

Для освобождения от произвольной постоянной C примем дополнительные условия.

При , , тогда

. (3.22)

Выражая C из (3.22) и подставляя в (3.21), получим

,

где - глубина погружения точки А.

Отсюда получаем формулу для определения гидростатического давления в точке на глубине h под свободной поверхностью (формула гидростатического давления)

. (3.23)

Разделив уравнение (3.21) на g, получим

.

Последнее уравнение для любых двух частиц одного и того же объема жидкости будет

.

Полученное уравнение называется основным уравнением гидростатики.

Из уравнения (3.23) следует, что давление возрастает по линейному закону с увеличением глубины погружения в несжимаемую жидкость.

Сопоставляя и , находим

.

Интегрируя, получим

или

.

Потенциальная функция в данном случае есть потенциальная энергия силы тяжести mgh, отнесенная к единице массы m

.