
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
ГИДРОСТАТИЧЕСКОЕ ДАВЛЕНИЕ И ЕГО СВОЙСТВА
Введем понятие о гидростатическом давлении. Рассмотрим объем жидкости, находящейся в равновесии. Разделим его плоскостью BC на две произвольные части I и II. Первую часть отбросим (рис. 3.2), а для сохранения
 равновесия части II суммарное воздействие на нее отброшенной части I заменим силой P. Тогда напряжение
равновесия части II суммарное воздействие на нее отброшенной части I заменим силой P. Тогда напряжение  будет называться средним гидростатическим давлением, действующим на площадку w, а предел отношения
будет называться средним гидростатическим давлением, действующим на площадку w, а предел отношения
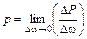
называется гидростатическим давлением в данной точке А. То есть гидростатическое давление есть напряжение, возникающее в жидкости, находящейся в равновесии. Гидростатическое давление p есть вектор. Единица измерения давления в системе СИ: Па=Н/м2.
Гидростатическое давление обладает следующими двумя основными свойствами.
1. Направление гидростатического давления всегда совпадает с направлением внутренней нормали к площадке, на которую оно действует. Это свойство легко доказать от противного. Проведем в жидком теле поверхность w, выделяющую некоторый объем II. Предположим, что в точке А (рис. 3.3) действует напряжение p, направленное не по нормали. Тогда мы можем его разложить на нормальное и касательное напряжения. Но касательные напряжения, обусловленные внутренним трением, могут возникать лишь при движении жидкости, а не при ее равновесии. Отсюда следует, что напряжение p может быть направлено лишь по нормали к площадке, на которую оно действует.
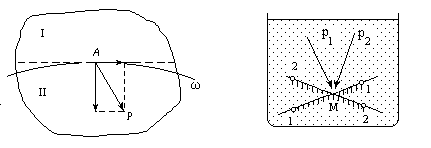
| Рис. 3.3 | Рис. 3.4 |
Так как принимается, что в жидкости не может быть растягивающих усилий (жидкость не оказывает сопротивления действию растягивающих сил), то направление гидростатического давления по внешней нормали также невозможно, поэтому оно может быть направлено лишь по внутренней нормали.
2. Величина гидростатического давления в данной точке не зависит от направления той площадки, по которой оно действует. Это значит, что если через точку М провести, например, две площадки 1-1 и 2-2 (рис. 3.4), то гидростатические давления на этих площадках по абсолютной величине будут одинаковы, т.е. 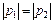 .
.
Для доказательства выделим в жидкости, находящейся в равновесии, элементарный тетраэдр, ребра которого 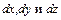 выходят из некоторой точки А и параллельны координатным осям x, y, z (рис. 3.5).
выходят из некоторой точки А и параллельны координатным осям x, y, z (рис. 3.5).
Пусть 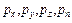 - средние гидростатические давления, действующие на гранях тетраэдра, площади которых равны
- средние гидростатические давления, действующие на гранях тетраэдра, площади которых равны 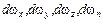 . Формулы для давлений будут определяться отношением силы, действующей на соответствующую грань, к ее площади, где индексы x, y, z, n показывают, какое направление является нормалью к данной площадке
. Формулы для давлений будут определяться отношением силы, действующей на соответствующую грань, к ее площади, где индексы x, y, z, n показывают, какое направление является нормалью к данной площадке
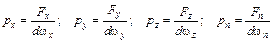 .
.
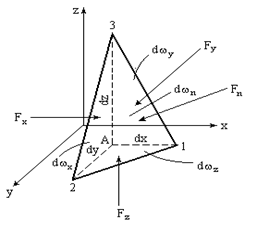
Рис. 3.5
Например, площадь 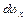 равна площади фигуры 2-3-А, а ось х нормальна к ней и т.д.
равна площади фигуры 2-3-А, а ось х нормальна к ней и т.д.
На элементарный тетраэдр, например, вдоль оси х действует также массовая сила тяжести 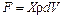 , где X - проекция ускорения массовой силы, приходящейся на единицу массы, на ось x; rdV - масса элементарного тетраэдра. Аналогичные силы будут действовать и по другим координатным осям.
, где X - проекция ускорения массовой силы, приходящейся на единицу массы, на ось x; rdV - масса элементарного тетраэдра. Аналогичные силы будут действовать и по другим координатным осям.
По условию жидкость находится в равновесии, поэтому массовые и поверхностные силы должны уравновешиваться. Составим уравнение равновесия сил в проекции на ось x
 . (3.1)
. (3.1)
Выражая Fx и Fn из приведенных выше формул и подставляя в (3.1), получим
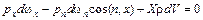 . (3.2)
. (3.2)
Так как  , то соотношение (3.2) примет вид
, то соотношение (3.2) примет вид
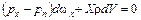 . (3.3)
. (3.3)
Величины площади dwx и объема тетраэдра dV будут определяться по формулам
 ; (3.4)
; (3.4)
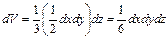 . (3.5)
. (3.5)
Подставляя (3.4), (3.5) в (3.3), получим
 .
.
Отсюда
 . (3.6)
. (3.6)
Переходя к пределу путем приближения площади dwn к точке А, получим dx=0. Тогда (3.6) примет вид
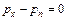 , (3.7)
, (3.7)
где Px и Pn уже не средние, а истинные гидростатические давления в точке А.
Из (3.7) получим  .
.
Составляя условия равновесия сил в проекциях на оси y и z, найдем
py =pn ; pz=pn. Отсюда
px=py=pz=pn . (3.8)
Из равенства (3.8) следует, что величина гидростатического давления в данной точке не зависит от направления площадки, на которую это давление действует. Таким образом, второе свойство гидростатического давления оказывается доказанным.
Дата добавления: 2015-04-18; просмотров: 298; Мы поможем в написании вашей работы!; Нарушение авторских прав |