ОСНОВНЫЕ ФИЗИКО-МЕХАНИЧЕСКИЕ СВОЙСТВА ЖИДКОСТИ

Жидкостями называют физические тела, легко изменяющие свою форму под действием самых небольших сил.

Различают два рода жидкостей.

1. Капельные (несжимаемые).

2. Газообразные (сжимаемые).

В гидравлике принимается, что жидкость представляет из себя сплошную среду. Для этого здесь полностью отвлекаются от внутренних молекулярных движений в жидкости и рассматривают движения элементарных объемов, достаточно больших по сравнению с расстояниями между молекулами, благодаря чему движение жидкости рассматривается не как движение большого количества дискретных частиц - молекул, а как движение непрерывной среды с непрерывно меняющимися свойствами (давление, плотность и т.д.).

Такой прием рассмотрения движения жидкости открывает широкие возможности для использования дифференциального и интегрального исчислений к решению задач гидравлики, ибо только в случае непрерывных функций эти исчисления можно успешно применять.

Рассмотрим основные физико-механические свойства жидкости: плотность, удельный вес и удельный объем.

Выделим в жидкости некоторый объем DV. Пусть масса жидкости в этом объеме равна Dm. Тогда будет называться средней в данном объеме плотностью жидкости (если жидкость неоднородна).

Уменьшая DV до нуля, находя предел

,

получим истинное значение плотности в данной точке.

Об этом пределе можно вести речь, если только жидкость считать непрерывной сплошной средой. Таким образом, плотностью жидкой среды в данной точке называется предел, к которому стремится средняя плотность в данном объеме при стремлении этого объема к нулю.

Плотность – это масса единицы объема . Если тело однородно, то удельный вес – это вес единицы объема ; так как , то или , т.е. удельный вес прямо пропорционален плотности.

Единица измерения удельного веса в системе МКГСС – кгс/м³, в системе СИ - Н/м³= кг/(м²×с²). Аналогично единица измерения плотности в МКГСС - кгс×с²/м⁴, в СИ - н×с²/м⁴ = кг/м³. Например, для воды при g = 9,81 м/с²
g = 1000 кгс/м³, r = 1000/9,81 = 101,9 кг×с²/м⁴. Отметим, что числовое значение удельного веса, выраженного в кгс/м³, совпадает с числовым значением плотности, выраженной в кг/м³.

Удельный объем - объем единицы массы - есть величина, обратная плотности . Как показывают многочисленные исследования, плотность жидкости в точке есть функция давления и температуры в данной точке: . Эта зависимость носит название уравнения состояния.

Опыт показывает, что плотности капельных жидкостей с ростом давления изменяются очень мало. Например, при увеличении давления от 1 до
100 атм первоначальный объем воды уменьшается на 0,5% и, следовательно, плотность увеличивается на 0,5%. Плотность газов с ростом давления значительно растет. Плотность капельных жидкостей с ростом температуры изменяется, как правило, незначительно.

Для нефти и нефтепродуктов по формуле Менделеева имеем

,

где r₁₅ - плотность при t = 15 ⁰С; b - коэффициент объемного расширения.

При увеличении t от 15 ⁰C до 100 ⁰С плотность нефти уменьшается примерно на 7%. Плотность газов значительно меняется с температурой. Так, для идеальных газов имеет место уравнение Клапейрона или , откуда , т.е. плотность газов находится в обратно пропорциональной зависимости от температуры.

§ 2.2. ВЯЗКОСТЬ. ЗАКОН НЬЮТОНА ДЛЯ ВНУТРЕННЕГО
ТРЕНИЯ В ЖИДКОСТИ

Вязкостью называется способность жидкости оказывать сопротивление сдвигающим усилиям. Это свойство жидкости проявляется лишь при ее движении. Допустим, что некоторое количество жидкости заключено между двумя плоскими неограниченными параллельными пластинами (рис. 2.1). Расстояние между ними обозначим через n. Пусть верхняя пластина движется относительно нижней с некоторой скоростью u.

Опыт показывает, что слой жидкости, непосредственно прилегающий к стенке, прилипает к ней. Отсюда следует, что скорость движения жидкости, прилегающей к нижней стенке, равна нулю, а к верхней - u. Промежуточные слои движутся со скоростью, постепенно возрастающей от 0 до u.

Таким образом, существует разность скоростей между соседними слоями и возникает взаимное скольжение слоев, которое приводит к возникновению силы внутреннего трения.

Чтобы перемещать одну пластину относительно другой, необходимо приложить к движущейся пластине некоторую силу T, равную силе сопротивления жидкости в результате внутреннего трения. Ньютон установил, что эта сила пропорциональна относительной скорости u, поверхности соприкосновения S и обратно пропорциональна расстоянию между пластинами n, т.е.

,

где m - коэффициент пропорциональности.

Для большего уточнения этой зависимости ее следует отнести к бесконечно малому расстоянию между слоями жидкости, тогда

,

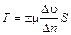где D u - относительная скорость движения соседних слоев; Dn - расстояние между ними.

Или в пределе

.

Последнее выражение носит название закона Ньютона для внутреннего трения. Знак плюс или минус принимается в зависимости от знака градиента скорости .

Так как - есть касательное напряжение сдвига, то закону Ньютона можно придать более удобный вид

.

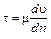Касательное напряжение, возникающее в жидкости, пропорционально градиенту скорости в направлении, перпендикулярном вектору скорости, и к площадке, по которой оно действует.

Коэффициент пропорциональности m характеризует физические свойства жидкости и называется динамическим коэффициентом вязкости. Из формулы Ньютона следует

.

Из этого выражения вытекает физический смысл коэффициента μ: если , то .

В гидродинамике вводят в рассмотрение величину

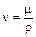[м²/с],

называемую кинематическим коэффициентом вязкости.

Динамический коэффициент вязкости m с ростом температуры уменьшается, а с увеличением давления увеличивается. Однако влияние давления для капельных жидкостей незначительно. Динамический коэффициент вязкости газов с увеличением температуры возрастает, а от давления изменяется незначительно.

Закон Ньютона для внутреннего трения в жидкости существенно отличается от законов трения твердых тел. В твердых телах существует трение покоя, кроме того, сила трения пропорциональна нормальному давлению и мало зависит от относительной скорости движения. В жидкости, подчиняющейся закону Ньютона, при отсутствии относительной скорости движения слоев сила трения отсутствует. Сила трения не зависит от давления (нормального напряжения), а зависит от относительной скорости перемещения слоев. Жидкости, подчиняющиеся закону Ньютона, называются ньютоновскими жидкостями. Однако существуют жидкости, которые не подчиняются этому закону (аномальные жидкости). К их числу относятся различного вида эмульсии, коллоидные растворы, представляющие собой неоднородные тела, состоящие из двух фаз (твердой и жидкой).

Так, глинистые растворы, применяемые при бурении нефтяных скважин, некоторые сорта нефтей вблизи температуры их застывания не подчиняются закону Ньютона. Опытами установлено, что в подобных жидкостях движение наступает после того, как касательные напряжения достигнут некоторого значения, называемого начальным напряжением сдвига.

Для таких жидкостей справедлива более общая зависимость для t (формула Бингема)

,

где h - коэффициент структурной вязкости.

Таким образом, эти жидкости при напряжении t< t₀ ведут себя как твердые тела и начинают течь лишь при t³ t₀. В дальнейшем градиент скорости пропорционален не t, а разнице t-t₀.

Графически зависимость между и t изображается кривой 1 для ньютоновских жидкостей и кривой 2 - для аномальных жидкостей (рис. 2.2).

При движении структурных жидкостей по трубопроводу наблюдаются три режима их движения: 1) структурный; 2) ламинарный; 3) турбулентный.

Для начала движения необходим некоторый начальный перепад давления в трубопроводе Dp₀, после чего жидкость отделяется от стенок и начинает двигаться как одно целое (как твердое тело - структурный режим).

При увеличении перепада давления Dp будет увеличиваться скорость движения раствора и вблизи стенок начнет развиваться ламинарный режим течения. По мере дальнейшего увеличения скорости область ламинарного режима будет расширяться, затем структурный режим полностью переходит в ламинарный.

При дальнейшем увеличении скорости ламинарный режим переходит в турбулентный (см. § 6.1).

§ 2.3. Зависимость вязкости от температуры и давления. Вискозиметры

Вязкость капельной жидкости в значительной степени зависит от температуры и в меньшей степени – от давления жидкости. Зависимостью вязкости от давления в большинстве случаев пренебрегают. Например, при давлениях до 50 атм вязкость изменяется не более, чем на 8,5 %. Исключением является вода при температуре 25 °С – ее вязкость с увеличением давления незначительно уменьшается. Другая особенность воды состоит в том, что ее плотность с уменьшением температуры до + 4 °С возрастает, а при дальнейшем уменьшении температуры (от +4 °С до 0 °С) уменьшается. Этим объясняется тот факт, что вода замерзает с поверхности. При температуре около
0 °С она имеет наименьшую плотность и слои жидкости, имеющие такую температуру, как наиболее легкие всплывают на поверхность, где и происходит замерзание воды, если ее температура оказывается меньшей 0 °С.

При атмосферном давлении вязкость воды в зависимости от температуры определяется по формуле Пуазейля

где 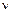- кинематический коэффициент вязкости;

- динамический коэффициент вязкости;

- плотность воды при данной температуре;

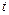- температура воды.

Вязкость жидкости определяют при помощи приборов, называемых вискозиметрами. Для жидкостей, более вязких, чем вода, применяют вискозиметр Энглера. Этот прибор состоит из емкости с отверстием, через которое при температуре 20 °С определяют время слива дистиллированной воды Т₀ и жидкости Т, вязкость которой требуется определить. Отношение величин Т и Т₀ составляет число условных градусов Энглера

.

После определения вязкости жидкости в условных градусах Энглера кинематический коэффициент вязкости находится по следующей эмпирической формуле

, см²/с.

Полученные по этой формуле значения 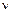хорошо согласуются с опытными данными.

Задачи

Задача 1. Определить изменение объема воды в резервуаре при нагреве ее от до . Первоначальный объем воды . Коэффициент объемного расширения в интервале температур ─ при давлении 10⁵ Па .

Решение. Коэффициент температурного расширения капельных жидкостей, определяющий относительное изменение объема жидкости при увеличении температуры на 1 градус, находится по формуле

где -первоначальный объем жидкости; -изменение объема жидкости при увеличении ее температуры на величину .

Из формулы для имеем

.

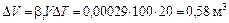Задача 2. Определить изменение плотности воды при увеличении ее температуры от до .

Решение. Изменение плотности можно найти по следующей приближенной формуле

,

где - плотность при температуре ; -коэффициент температурного расширения.

Отсюда

.

Задача 3. Определить кинематическую и динамическую вязкость воды при температуре (давление ).

Решение. Для определения кинематической вязкости используем формулу

Формула для определения динамической вязкости воды имеет вид

Сделаем проверку, определив кинематическую вязкость по формуле

,

где -плотность воды при температуре .

Отсюда

.

Задача 4. Определить кинематическую и динамическую вязкость нефти при температуре . Вязкость, определенная по вискозиметру Энглера, составляет .

Решение. Плотность нефти при температуре 20⁰ С составляет . Кинематическую вязкость найдем по формуле Убеллоде

Динамическая вязкость будет

Пуаз (П).

Задача 5. Определить изменение плотности нефти при сжатии ее от Па до Па, если коэффициент объемного сжатия нефти Па ^–1.

Решение. Коэффициент объемного сжатия определяется по формуле

или , (а)

где - объем жидкости при давлении ; -изменение объема жидкости при ее сжатии.

Разность давлений находится по формуле

Па.

Плотность нефти определяется из соотношения

,

где -масса нефти.

Так как масса нефти в процессе сжатия остается неизменной, то

, (б)

где

. (в)

Формула (в) с учетом (а) будет

. (г)

Подставляя (г) в (б), получим

.

Отсюда следует, что плотность нефти с изменением давления от 10⁵ Па до 10⁶ Па изменяется незначительно.

Глава 3