ПОТЕНЦИАЛ МАССОВЫХ СИЛ

Умножая уравнения Эйлера (3.12) соответственно на dx, dy, dz и почленно складывая, получим

. (3.13)

Так как p= f (x, y, z,), то полный дифференциал этой функции будет

. (3.14)

Следовательно, правая часть уравнения (3.13) есть полный дифференциал

. (3.15)

Равенство (3.15) имеет смысл лишь в том случае, если левая его часть есть также полный дифференциал какой-то функции. Обозначим эту функцию через . Тогда полный дифференциал ее будет

. (3.16)

Примем, что

. (3.17)

Из сопоставления (3.15), (3.17) получим

X= ; Y= ; Z= .

Функцию называют потенциальной функцией, а силы для которых эта функция существует, - силами, имеющими потенциал.

Отсюда приходим к следующему выводу: жидкость может находиться в равновесии только под действием массовых сил, имеющих потенциал, так как только такие силы удовлетворяют уравнениям равновесия Эйлера.

§ 3.5. ИНТЕГРАЛ УРАВНЕНИЙ ЭЙЛЕРА ДЛЯ НЕСЖИМАЕМОЙ
ЖИДКОСТИ

Проинтегрируем уравнение (3.17) при r=const

.

Отсюда

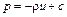, (3.18)

где c - постоянная интегрирования. Полагая, что при p=p₀ потенциальная функция u = u₀, будем иметь

.

Отсюда

_. (3.19)

Подставляя (3.19) в (3.18), получим

или

.

Последнее соотношение является интегралом уравнений Эйлера для несжимаемой капельной жидкости.

Так как величина не зависит от давления p₀ и определяется лишь системой массовых (но не поверхностных) сил, то отсюда следует, что насколько изменится давление p₀, на столько же изменится и давление p в любой точке жидкости. Отсюда можно сформулировать закон Паскаля: давление, производимое на поверхность капельной жидкости, находящейся в равновесии, передается всем ее частицам без изменения его величины.