ГИДРОСТАТИЧЕСКИЙ НАПОР И ЭНЕРГЕТИЧЕСКИЙ ЗАКОН ДЛЯ ЖИДКОСТИ, НАХОДЯЩЕЙСЯ В РАВНОВЕСИИ

При выводе основного уравнения гидростатики выше (см. п. 3.7) было получено дифференциальное уравнение вида

.

Прежде чем интегрировать это уравнение, представим его в следующем виде

или

.

Проинтегрировав, получим

.

Величина представляет ту высоту, на которую поднялась бы жидкость в пьезометре, если бы верхний конец его находился под нулевым давлением p = 0 (рис. 3.12).

Таким образом, это есть высота, соответствующая абсолютному давлению в жидкости. Она называется приведенной (высота h₂).

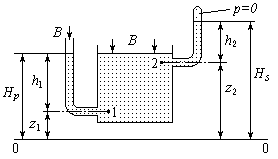
Рис. 3.12

- геометрическая высота выбранной точки над условной плоскостью сравнения 0 - 0. Отсюда

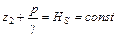. (3.24)

Уравнение (3.24) показывает, что сумма двух высот и для любой точки жидкости остается постоянной. Эта сумма называется абсолютным (полным) гидростатическим напором.

Если конец пьезометра соединить с атмосферой при давлении B, то уравнение (3.24) примет вид

. (3.25)

Сумма и называется гидростатическим напором, а величина - пьезометрическим напором.

Горизонтальная плоскость, проведенная на высоте , называется плоскостью гидростатического или пьезометрического напора, а 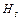- плоскостью абсолютного (полного) напора. Очевидно, что .

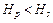Выражениям (3.24) и (3.25) можно придать простой энергетический смысл. Рассмотрим частицу жидкости массой m. Ее потенциальная энергия относительно плоскости 0 - 0 будет mgz. Кроме того, под действием давления p частица может подняться на высоту 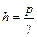, т.е. обладает потенциальной энергией давления, равной

.

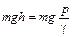Таким образом, полный запас потенциальной энергии частицы будет

.

Разделив последнее соотношение на mg, получим

,

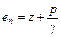где .

Отсюда следует, что высота z - есть удельная потенциальная энергия положения частицы, а - удельная потенциальная энергия давления.

Величина

является полной удельной потенциальной энергией частицы.

Последнее соотношение называется энергетическим законом для жидкости, находящейся в равновесии.

Для всех точек данного объема покоящейся жидкости удельная потенциальная энергия одинакова. Эти утверждения справедливы как для полного 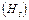, так и для пьезометрического напоров.