СИЛА ДАВЛЕНИЯ ЖИДКОСТИ НА КРИВОЛИНЕЙНУЮ ПОВЕРХНОСТЬ ПРОИЗВОЛЬНОЙ ФОРМЫ

Рассмотрим криволинейную поверхность произвольной формы, отделяющую капельную жидкость от газа, например, часть поверхности стенки сосуда (рис. 3.15).

На каждую из элементарных площадок dw_n криволинейной поверхности действует элементарная сила, направленная по нормали к площадке и равная dF. В общем случае все эти элементарные силы образуют систему сил, произвольно расположенных в пространстве. Такая система, как известно из теоретической механики, приводится к одной силе , называемой главным вектором, и к одной паре сил, момент которой называется главным моментом.

Рис. 3.15

Здесь - радиус-вектор площадки относительно центра моментов;

´ - знак векторного произведения.

В частных случаях эта система приводится к одной силе, называемой равнодействующей.

В дальнейшем определим лишь величину главного вектора сил давления. Как известно, для определения главного вектора по величине и по направлению достаточно вычислить три его проекции на оси координат. Тогда величина его будет

,

а направление определяется соотношениями

; ; .

Рассмотрим сначала определение проекций вектора силы давления на горизонтальные оси. Определим . Давление на элементарную площадку dw_n на основании формулы гидростатического давления . Напомним, что величина этого давления не зависит от направления площадки по 2-му свойству гидростатического давления. Элементарная сила определяется по формуле

.

Ее проекция на ось x

.

Учитывая, что , получим

.

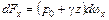Интегрируя, находим

.

Очевидно, . Второй интеграл равен статическому моменту площади w_x относительно оси 0y или

,

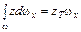где - глубина погружения центра тяжести вертикальной проекции криволинейной поверхности. Отсюда получим

.

Аналогично для другой горизонтальной проекции будем иметь

,

где относится к w_y.

Таким образом, горизонтальная проекция вектора силы давления равна произведению площади вертикальной проекции данной поверхности на величину гидростатического давления на глубине погружения центра тяжести этой проекции.

Для определения вертикальной проекции F_z аналогично составим интеграл

или

,

где - горизонтальная проекция .

Последнее соотношение перепишем в виде

.

Первый интеграл равен .

Второй интеграл

есть объем воды, заключенный между криволинейной поверхностью и ее проекцией на свободную поверхность - плоскость y0x . Этот объем называют объемом тела давления.

Тогда интеграл

равен весу тела давления. Отсюда

.

Таким образом, вертикальная проекция равна сумме произведения начального давления на горизонтальную проекцию криволинейной поверхности w_z и веса тела давления.

Нахождение горизонтальных проекций не составляет труда. Определение вертикальной проекции связано с нахождением объема или веса тела давления, на чем мы остановимся несколько подробнее.

§ 3.12. Частные случаи расчета сил, действующих
на криволинейные поверхности закономерных форм

Рассмотрим здесь только цилиндрические поверхности с образующей параллельной оси y (рис.3.16).

Задача в данном случае по существу сводится к нахождению тела давления и к определению направления веса тела давления. Вес тела давления может быть как положительный – направленный по оси 0z , так и отрицательный – направленный в сторону отрицательных z, т. е. вертикально вверх.

Рис. 3.16

Когда силы давления действуют на поверхность вниз, то и вес тела давления получается направленным вниз, т. е. положительным. Когда силы давления действуют на поверхность вверх (случай 3), то и вес тела давления направлен вверх, т.е. отрицателен. После нахождения G расчет ведется также, как было указано выше.

§ 3.13. Сила давления жидкости на плоскую стенку
произвольной формы

Пусть имеется фигура произвольной формы площадью w в плоскости 0l, наклоненной к горизонту под углом a (рис. 3.17).

Для удобства вывода формулы для силы давления жидкости на рассматриваемую фигуру повернем плоскость стенки на 90⁰ вокруг оси 0l и совместим ее с плоскостью чертежа. Выделим на рассматриваемой плоской фигуре на глубине h от свободной поверхности жидкости элементарную площадку dw. Тогда элементарная сила, действующая на площадку dw, будет

.

Интегрируя последнее соотношение, получим суммарную силу давления жидкости на плоскую фигуру

.

Учитывая, что , получим

или

.

Рис. 3.17

Последний интеграл равен статическому моменту площадки w относительно оси 0y, т.е.

,

где l_с - расстояние от оси 0y до центра тяжести фигуры. Тогда

.

Так как 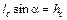, то

,

т. е. суммарная сила давления на плоскую фигуру равна произведению площади фигуры на гидростатическое давление в ее центре тяжести.

Точка приложения суммарной силы давления (точка d, рис 3.17) называется центром давления. Центр давления находится ниже центра тяжести плоской фигуры на величину эксцентриситета е. Последовательность определения координат центра давления и величины эксцентриситета изложена в § 3.15.

В частном случае вертикальной прямоугольной стенки получим (рис. 3.18)

.

В частном случае горизонтальной прямоугольной стенки будем иметь

.