ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ РАВНОВЕСИЯ ЖИДКОСТИ

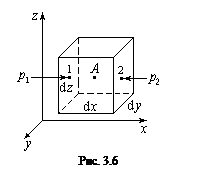Выделим в жидкости, находящейся в равновесии, элементарный параллелепипед с ребрами dx, dy, dz, параллельными осям координат x, y, z,
(рис. 3.6). Выберем в центре параллелепипеда точку А. Давление в этой точке будет . Так как это давление является непрерывной функцией координат, то, разлагая функцию в ряд Тэйлора в окрестности точки А с точностью до бесконечно малых первого порядка, получим следующие соотношения для давлений p₁ и p₂ в точках 1 и 2 на гранях параллелепипеда, перпендикулярных оси x

;

.

Давления в точках 1 и 2 можно также записать в виде отношения силы к площади

; , (3.9)

где F₁ и F₂ - силы, действующие в точках 1 и 2.

Запишем условие равновесия сил, действующих на элементарный параллелепипед, в проекции на ось x

, (3.10)

где F_m-массовая сила, определяемая по формуле

, (3.11)

где dm – масса элементарного параллелепипеда.

Подставляя (3.9), (3.11) в (3.10), получим

.

Подставляя формулы для p₁ и p₂, найдем

.

Отсюда

.

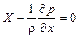Аналогичные уравнения можно получить, если спроектировать действующие на параллелепипед силы на оси y и z. В итоге будем иметь систему трех дифференциальных уравнений вида

(3.12)

где X, Y, Z, - проекции ускорений массовых сил, приходящихся на единицу массы.

Эти уравнения впервые были выведены Эйлером в 1755 г. и называются уравнениями равновесия жидкости Эйлера. Они показывают, что при равновесии жидкости массовые силы уравновешиваются соответствующими поверхностными силами.

В векторной форме эти уравнения имеют вид

,

где 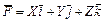; , , - орты координатных осей;

.

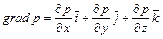При i = 1 j = k = 0; при j = 1 i = k = 0; при k = 1 i = j = 0.