УРАВНЕНИЕ НЕРАЗРЫВНОСТИ В ПЕРЕМЕННЫХ ЭЙЛЕРА В ДЕКАРТОВОЙ СИСТЕМЕ КООРДИНАТ

Уравнение неразрывности (сплошности) выражает закон сохранения массы и неразрывность течения. Для вывода уравнения выделим в массе жидкости элементарный параллелепипед с ребрами dx, dz, dz (рис. 4.10).

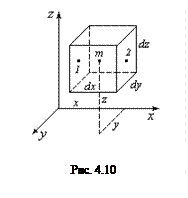Пусть точка m с координатами x, y, z находится в центре этого параллелепипеда. Плотность жидкости в точке m будет .

Подсчитаем массу жидкости, втекающей в параллелепипед и вытекающей из него через противоположные грани за время dt. Масса жидкости, втекающей через левую грань за время dt в направлении оси x, равна

,

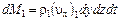где r₁ и (u_x)₁ - плотность и проекция скорости на ось x в точке 1.

Функция 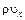является непрерывной функцией координаты x. Разлагая эту функцию в окрестности точки m в ряд Тэйлора с точностью до бесконечно малых первого порядка, для точек 1 и 2 на гранях параллелепипеда получим следующие ее значения

;

.

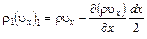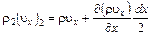Масса жидкости, вытекающей через правую грань за время 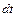в направлении оси x , будет

.

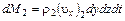Разность между массой втекающей и вытекающей жидкости в направлении оси x за время Dt будет равна

.

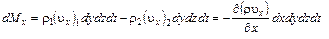Аналогично для осей y и z получим

;

.

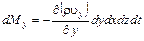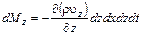Если жидкость сплошь заполняет рассматриваемый объем, то согласно закону сохранения массы сумма найденных разностей масс должна быть равна приращению массы жидкости в том же объеме, вызванному изменением плотности r за время dt, т.е.

.

Известно, что .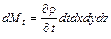

Подставляя значения dM_t , dM_x , dM_y , dM_z в уравнение закона сохранения масс, получим

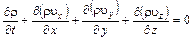. (4.6)

Так как

;

;

;

,

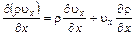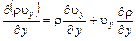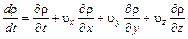то, подставляя последние соотношения в (4.6), будем иметь

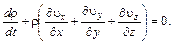(4.7)

Соотношение (4.7) является уравнением неразрывности сжимаемой жидкости. Этому уравнению можно придать вид

,

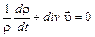где выражение в скобках называется дивергенцией вектора скорости.

Для установившегося движения частная производная от плотности по времени равна нулю 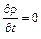, и уравнение (4.7) принимает вид

.

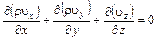В случае движения несжимаемой жидкости 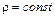и плотность от времени не зависит, т.е.

.

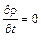Поэтому

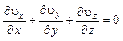(4.8)

или

.

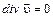Уравнение неразрывности для элементарной струйки имеет вид

,

т.е. массовые расходы во всех сечениях элементарной струйки одинаковы.

Для потока

.

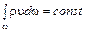Если жидкость несжимаема, то

; ; .

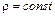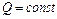Отсюда следует, что Q_{1 =} Q_2..

Так как

,

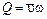то

.

Отсюда

,

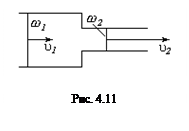
т.е. средние скорости потока обратно пропорциональны площадям живых сечений потока (рис. 4.11). Объемный расход Q несжимаемой жидкости остается постоянным вдоль канала.

§ 4.7. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ДВИЖЕНИЯ ИДЕАЛЬНОЙ
(НЕВЯЗКОЙ) ЖИДКОСТИ (УРАВНЕНИЯ ЭЙЛЕРА)

Невязкой или идеальной жидкостью называется жидкость, частицы которой обладают абсолютной подвижностью. Такая жидкость неспособна сопротивляться сдвигающим усилиям и поэтому касательные напряжения в ней будут отсутствовать. Из поверхностных сил в ней будут действовать только нормальные усилия.

Предел

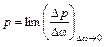
в движущейся жидкости называется гидродинамическим давлением. Гидродинамическое давление обладает следующими свойствами.

1. Оно действует всегда по внутренней нормали (сжимающее усилие).

2. Величина гидродинамического давления не зависит от ориентировки площадки (что доказывается аналогично второму свойству гидростатического давления).

На основании этих свойств можно считать, что . Таким образом, свойства гидродинамического давления в невязкой жидкости идентичны свойствам гидростатического давления. Однако величина гидродинамического давления определяется по уравнениям, отличным от уравнений гидростатики.

Для вывода уравнений движения жидкости выделим элементарный параллелепипед в массе жидкости с ребрами dx, dy, dz (рис. 4.12). Пусть точка m с координатами x,y,z находится в центре этого параллелепипеда. Давление в точке m будет . Компоненты массовых сил, отнесенных к единице массы, пусть будут X,Y,Z.

Запишем условие равновесия сил, действующих на элементарный параллелепипед, в проекции на ось x

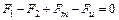, (4.9)

где F₁ и F₂ – силы гидростатического давления; F_m – равнодействующая массовых сил тяжести; F_и – равнодействующая сил инерции.

Рис. 4.12

Силы гидростатического давления равны произведению гидростатических давлений в центрах тяжести элементарных площадок (в точках 1 и 2) на их площади

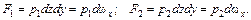
Давления p₁ и p₂ определяются по формулам (см. § 3.3.)

.

Эти формулы показывают насколько давление p в точке А отличается от давлений в точках 1 и 2.

Формула для определения равнодействующей массовых сил имеет вид

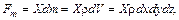
где – масса элементарного параллелепипеда.

Равнодействующая сил инерции определяется в виде произведения массы элементарного параллелепипеда на его ускорение

.

Знак минус указывает на то, что сила инерции направлена противоположно направлению оси x.

Подставляя F₁, F₂, F_m, F_и в (4.9), получим

.

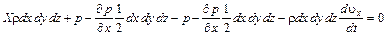Отсюда

.

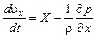Если рассматривать условие равновесия сил, действующих на элементарный параллелепипед в проекциях на оси y и z, то получим еще два уравнения

;

.

Записывая последние три уравнения в развернутом виде, получим уравнения движения Эйлера для идеальной невязкой жидкости, выведенные им в 1775 г.

;

;

.

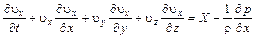В случае несжимаемой невязкой жидкости ( ) система уравнений Эйлера имеет четыре неизвестных: 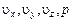. Так как уравнений 3, а неизвестных 4, то система уравнений Эйлера в данном случае оказывается незамкнутой. Для того чтобы она была замкнутой, необходимо добавить еще одно уравнение. Таким уравнением будет уравнение неразрывности

.

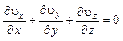Для того чтобы получить конкретные однозначные решения замкнутой системы дифференциальных уравнений, необходимо задать условия однозначности, которые включают: 1) геометрические условия (линейные размеры рассматриваемой области); 2) физические условия (физические константы, характеризующие жидкость); 3) начальные условия (значения искомых функций в начальный момент времени); 4) граничные условия (значения искомых функций на границе области). Система дифференциальных уравнений с условиями однозначности представляют полную математическую постановку задачи.

§ 4.8. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ДВИЖЕНИЯ ВЯЗКОЙ ЖИДКОСТИ
(УРАВНЕНИЯ НАВЬЕ-СТОКСА)

Вязкой называется такая жидкость, которая при своем движении оказывает сопротивление сдвигающим усилиям. Все жидкости, существующие в природе, являются вязкими. Поэтому вязкую жидкость называют еще реальной жидкостью. Рассмотрим поверхностные силы, действующие в вязкой жидкости.

В вязкой жидкости ввиду наличия сил трения возникают касательные напряжения. Поэтому напряжения, действующие на площадку, могут быть направлены как угодно по отношению к ней, а не обязательно по нормали.

В вязкой жидкости различают два рода напряжений (рис.4.13).

Рис. 4.13

1.Нормальное напряжение p_nn - проекция p_n на нормаль n в данной точке поверхности.

2.Касательное напряжение t - проекция p_n на касательную плоскость к поверхности в данной точке. Касательные напряжения имеют место лишь при движении вязкой жидкости.

Рассмотрим теперь схему поверхностных сил, действующих в вязкой жидкости (рис.4.14). Первый индекс при p указывает нормаль к площадке, на которую действует напряжение, второй - ось, на которую оно спроектировано.

Выделим в движущейся жидкости элементарный параллелепипед с ребрами, параллельными осям x, y, z и рассмотрим поверхностные силы, действующие на его гранях.

Условимся считать нормальное напряжение положительным в том случае, когда оно направлено по внешней нормали. То есть в данном случае нормальное напряжение направлено противоположно давлению. Нормальное напряжение - это реакция жидкого элемента на воздействие окружающей его жидкости.

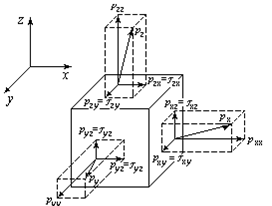
Рис.4.14

В вязкой жидкости, в противоположность невязкой, напряжение зависит от ориентации площадки в данной точке. Однако, как строго доказывается в теоретической гидромеханике, сумма всех нормальных напряжений 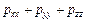в данной точке не зависит от ориентации площадки и, следовательно, эта сумма является скалярной функцией только координат точки и времени, в связи с чем вводится новое понятие о гидромеханическом давлении

, .

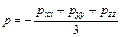Гидромеханическим давлением в вязкой жидкости называется давление, величина которого равна среднему арифметическому из величин любых трех нормальных напряжений в данной точке. Знак «минус» берется потому, что ,направленные по внешней нормали, всегда отрицательны, а p - должно быть положительным, как это обычно принимают в гидравлике. Таким образом, понятия гидромеханического давления в вязкой жидкости и гидродинамического давления в невязкой идеальной жидкости существенно различны.

Дадим упрощенный вывод уравнений движения вязкой жидкости применительно лишь к частному случаю несжимаемой жидкости. Рассмотрим вначале одномерное движение жидкости в направлении, параллельном оси Ox.

Выделим в потоке движущейся жидкости элементарный параллелепипед с ребрами dx,dy,dz (рис.4.15). Соотношение (4.9) для сил, действующих на элементарный параллелепипед, в данном случае будет

, (4.10)

где F_тр – сила трения, определяемая по формуле

.

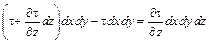По закону Ньютона для касательного напряжения τ имеем

.

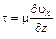Отсюда сила трения будет равна

.

Формулы для сил F₁, F₂, F_m, F_и смотреть в § 4.7. Подставляя эти силы и силу трения в (4.10), получим

.

Отсюда

,

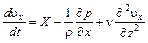где .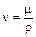

В общем случае движения в трехмерном пространстве, когда u_x изменяется по всем направлениям, а не только в направлении оси z, проекция силы трения на ось x определится более сложным выражением

.

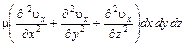Тогда уравнение движения в проекции на ось x будет

.

Или для всех трех осей x, y, z получим в развернутом виде

;

;

.

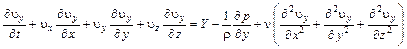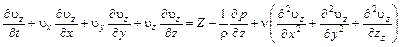Последние три уравнения называются уравнениями Навье-Стокса для вязкой несжимаемой жидкости.

Или в векторной форме

,

где

;

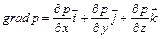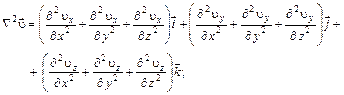
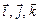- орты координатных осей (см. § 3.3).

Уравнения Навье-Стокса являются основными в гидромеханике вязкой жидкости. Но они определяют течение реальной вязкой жидкости вполне лишь тогда, когда подтверждается закон Ньютона о внутреннем трении в жидкости.

Добавим к полученным уравнениям движения уравнение неразрывности для несжимаемой жидкости

.

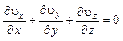Полагая, что внешние массовые силы X, Y, Z заданы, получим систему четырех уравнений с четырьмя неизвестными функциями 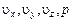. Следовательно, получена замкнутая система уравнений.

Принципиально эта система при заданных условиях однозначности дает возможность строгого решения задачи о движении вязкой несжимаемой жидкости. Однако аналитические решения уравнений Навье-Стокса найдены лишь для весьма ограниченного круга частных случаев.