ФИЗИЧЕСКИЙ И ГЕОМЕТРИЧЕСКИЙ СМЫСЛ УРАВНЕНИЯ БЕРНУЛЛИ. НАПОР ЖИДКОСТИ

Уравнению Бернулли можно дать два различных истолкования: физическое и геометрическое.

С физической точки зрения уравнение Бернулли есть выражение закона сохранения энергии для движущейся жидкости.

Действительно, рассмотрим величину

.

Эта сумма 3-х слагаемых называется полным напором жидкости или гидродинамическим напором.

С физической точки зрения напор есть механическая энергия жидкости, отнесенная к единице веса жидкости. Для того чтобы это показать, рассмотрим жидкость, движущуюся по трубопроводу (рис.4.16). Выделим в движущейся жидкости частицу M с массой m, веса . Потенциальная энергия этой частицы в поле силы тяжести по отношению к плоскости сравнения 0-0 будет mgz, а потенциальная энергия, отнесенная к единице веса, будет

,

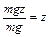т.е. z - есть удельная потенциальная энергия положения частицы жидкости - энергия, отнесенная к единице веса.

Под действием давления p частица жидкости М может подняться на высоту и, следовательно, совершить работу (рис.4.17)

,

т.е. она обладает потенциальной энергией давления в размере

.

Потенциальная энергия давления, отнесенная к единице веса, будет

,

т.е. - есть удельная потенциальная энергия давления частицы жидкости – энергия, отнесенная к единице веса жидкости.

Кроме того, выделенная частица обладает скоростью и, следовательно, имеет кинетическую энергию, равную .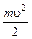

Кинетическая энергия, отнесенная к единице веса, будет

.

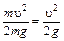Напор жидкости

будет, следовательно, равен полной энергии частицы жидкости, отнесенной к единице веса.

Таким образом, физическое истолкование уравнения Бернулли для элементарной струйки идеальной жидкости заключается в том, что для любых сечений 1 и 2 полная удельная энергия остается неизменной:

или

.

Уравнению Бернулли можно дать наглядное геометрическое истолкование. Для этого снова рассмотрим отдельные члены суммы

,

где z – геометрическая высота данной частицы жидкости над условной плоскостью сравнения.

- пьезометрическая высота – высота, на которую поднимется жидкость в пьезометре.

- скоростная высота - высота, на которую поднимется жидкость, имея начальную скорость u.

Таким образом, с геометрической точки зрения уравнение Бернулли в любом сечении элементарной струйки идеальной жидкости представляет собой сумму 3-х высот: геометрической, пьезометрической и скоростной, которая остается неизменной.

График уравнения Бернулли для элементарной струйки идеальной жидкости представлен на рис. 4.18.

Если сечение струйки увеличивается, то скорость падает, а давление возрастает, т.е. энергия, сохраняясь в целом, переходит из одного вида в другой (кинетическая энергия переходит в потенциальную и наоборот).

§ 4.11. УРАВНЕНИЕ БЕРНУЛЛИ ДЛЯ ЭЛЕМЕНТАРНОЙ
СТРУЙКИ РЕАЛЬНОЙ ЖИДКОСТИ

В идеальной жидкости, в отличие от реальной, отсутствуют силы внутреннего трения (отсутствует вязкость). Благодаря вязкости в реальной жидкости происходят потери механической энергии потока на трение внутри жидкости и о стенки канала. При этом происходит рассеивание (диссипация) энергии. Энергия, потерянная на трение, превращается в теплоту и идет на пополнение запаса внутренней энергии жидкости, а часть ее отводится в виде тепла через стенки канала.

Внутренняя энергия жидкости не может быть непосредственно использована для приведения жидкости в движение и поэтому в гидравлике рассматривается как потеря механической энергии (потеря напора).

Для реальной жидкости равенство нарушается и вместо него имеем 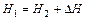, где 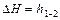– потеря напора на участке 1-2. Тогда для элементарной струйки реальной жидкости уравнение Бернулли примет вид

.

Таким образом, полный напор вдоль струйки реальной жидкости уменьшается. Для характеристики относительного изменения полного напора на единицу длины вводится понятие о гидравлическом уклоне

.

Например, на прямом участке трубопровода 1-2

,

где l_1-2 - длина участка 1-2.

Таким образом, гидравлическим уклоном называется отношение потери напора к длине, на которой она происходит.

Кроме того вводится еще понятие о пьезометрическом уклоне

.

Пьезометрический уклон может быть положительным, равным нулю и отрицательным.