УРАВНЕНИЕ БЕРНУЛЛИ ДЛЯ ПОТОКА РЕАЛЬНОЙ ЖИДКОСТИ

Применение уравнения Бернулли, выведенного для отдельной струйки, для потока жидкости затрудняется неравномерностью распределения скоростей по живому сечению потока, наличием поперечных составляющих продольной скорости и влиянием центробежных сил. В связи с этим необходимо установить характеристику потоков, для которых можно применять уравнение Бернулли, а также предложить способ учета неравномерности скоростей в живых сечениях потока.

Для решения этих вопросов в гидравлике выделяется так называемое плавно изменяющееся движение (рис. 4.19, 4.20), которое характеризуется следующими особенностями.

1. Угол расхождения соседних струек, а, следовательно, и поперечные составляющие скоростей в живых сечениях потока настолько малы, что ими можно пренебречь и рассматривать течение как происходящее только с продольной скоростью.

2. Кривизна линий тока настолько мала, а радиусы закруглений настолько велики, что центробежными силами в таких потоках можно пренебречь.

3. Кривизна живых сечений при неравномерном распределении скорости настолько невелика, что их можно рассматривать как плоские.

4. Гидродинамическое давление в живых сечениях распределяется по законам гидростатики, т.е. сумма z + p/g = const для всех точек данного живого сечения. Следовательно, уровень в пьезометрах при плавно-изменяющемся движении во всех точках живого сечения потока будет одним и тем же (рис. 4.21).

В случае плавноизменяющегося движения уравнение Бернулли для элементарной струйки можно распространить и на поток с поперечным сечением конечных размеров, скорости в различных точках которого различны. Однако в гидравлике обычно расчеты ведутся по средним скоростям. Для приведения результатов расчетов по средним скоростям в соответствие с расчетами по действительным скоростям вводятся некоторые поправочные коэффициенты (коэффициент Кориолиса, см. ниже).

Таким образом, плавноизменяющееся движение можно считать практически одномерным, т.е. положить 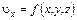, направив ось x параллельно потоку. Отсюда u_y»0; u_z»0. Тогда уравнения Навье-Стокса примут вид

;

;

.

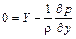Последние два уравнения переходят в уравнения гидростатики Эйлера, а это означает, что в плоскости y0z давления распределяются по закону гидростатики.

Распространим уравнение Бернулли для элементарной струйки реальной жидкости в виде

(4.15)

на поток реальной жидкости.

Правая и левая части этого уравнения есть удельная энергия жидкости, т.е. энергия, отнесенная к единице веса. Весовой расход элементарной струйки определяется по формуле

,

где dw - сечение элементарной струйки; 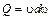- объемный расход.

Умножая обе части уравнения (4.15) на dG, получим не удельную, а полную энергию элементарной струйки в сечениях 1 и 2 и полную потерю этой энергии между сечениями 1 и 2 в единицу времени, т.е. ,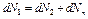

где - энергия струйки в 1-м сечении;

- энергия струйки во 2-м сечении;

- потеря энергии между 1-м и 2-м сечением.

Или

.

Для того чтобы получить подобные соотношения мощностей для всего потока

,

необходимо произвести интегрирование

. (4.16)

Преобразуем эти интегралы

.

Так как при плавноизменяющемся движении , то во всех точках данного сечения , .

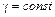Аналогично

.

Запишем третий интеграл в левой части соотношения (4.16) в виде

,

т.е. выразим его как произведение некоторого коэффициента a на скоростной напор, подсчитанный по средней скорости потока и на весовой расход жидкости .

Коэффициент a носит название коэффициента кинетической энергии потока или коэффициента Кориолиса. Таким образом, a представляет отношение кинетической энергии потока к кинетической энергии, вычисленной в предположении, что скорости всех точек живого сечения потока равны средней скорости потока, т.е.

; (4.17)

;

;

.

Кроме того из (4.17) следует

.

Отсюда заключаем, что коэффициент a характеризует неравномерность распределения скоростей по сечению потока. Для ламинарного режима
a ≈ 2, для турбулентного режима a » 1,05 - 1,1.

Существенно большее значение a для ламинарного режима течения по сравнению с турбулентным объясняется большей неравномерностью скорости в поперечном сечении потока при ламинарном режиме (см. профили скоростей ламинарного и турбулентного режимов течения, приведенные на
рис. 6.17).

Последний интеграл в (4.16) будет .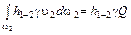

Тогда уравнение Бернулли для потока примет вид

.

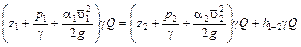Поделив на весовой расход жидкости обе части уравнения, получим соотношение для удельных энергий потока

.

Обычно для упрощения гидравлических расчетов трубопроводов для турбулентных потоков принимают a = 1 и уравнение Бернулли для потока будет иметь вид

.

§ 4.13. ГРАФИческая иллюстрация УРАВНЕНИЯ БЕРНУЛЛИ
ДЛЯ ПОТОКА РЕАЛЬНОЙ ЖИДКОСТИ

Рассмотрим распределение напоров в трубопроводе, имеющем сужение в средней его части (рис. 4.22). Выделим три характерных сечения, в которых расположим пьезометры и трубки Пито (описание трубок см. § 4.14).

На рис.4.22 при течении жидкости в трубопроводе могут быть выделены следующие характерные линии:

I - линия геометрических напоров;

II - пьезометрическая линия;

III - линия полного напора.

h_1-2, h_1-3 - потеря напора соответственно во втором и третьем сечениях.

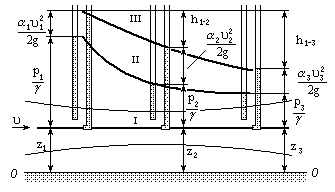
Рис. 4.22

Применительно к рис. 4.22 уравнение Бернулли запишется в виде

.

На рис. 4.22 отмечены все члены уравнения Бернулли. В частности, видно, что пьезометрический напор в узком сечении уменьшается, а скоростной напор 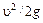- возрастает. Максимальная потеря напора имеет место в третьем сечении ( ) (потери на трение и в местных сопротивлениях см. гл. 6).

§ 4.14. ПРАКТИЧЕСКОЕ ПРИМЕНЕНИЕ УРАВНЕНИЯ БЕРНУЛЛИ

Уравнение Бернулли имеет широкое применение во многих гидравлических расчетах и для объяснения многих гидравлических явлений. В частности, оно может быть использовано для измерения давления и скорости движущейся жидкости. Для измерения давления используется пьезометр (прямая трубка на рис.4.23). Для измерения скорости совместно с пьезометром используется трубка Пито - трубка полного напора. Она представляет собой трубку, изогнутую под прямым углом и установленную навстречу потоку.

Уровень жидкости в пьезометре равен .

Разность уровней в пьезометре и в трубке полного напора будет равна скоростному напору .

Действительно, напишем уравнение Бернулли для точек А и В

.

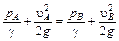Так как , , , 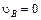то

,

где - высота жидкости в трубке полного напора; - высота жидкости в пьезометре.

Отсюда

.

Тогда

.

Или

,

где φ>1 - коэффициент, определяемый для каждой трубки опытным путем. За счет вязкости жидкости и других отклонений от идеального случая преобразования энергии и поэтому чтобы не получать пониженных значений скоростей,φ>1.

§ 4.15. ТРУБКА ПРАНДТЛЯ

Дальнейшим усовершенствованием трубки Пито является трубка Прандтля. В этом приборе объединяются трубка Пито и пьезометр (рис.4.24). Роль трубки Пито здесь выполняет трубка 2 (она направлена навстречу потоку), а пьезометра – трубка 1 (отверстия в этой трубке находятся параллельно направлению потока).

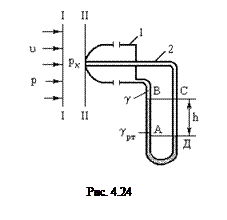Пусть в сечении I имеем давление и скорость набегающего потока p и v. В сечении II давление на входе в трубку 2 равно р_к (скорость u_к здесь равна нулю). Записывая уравнение Бернулли для сечений I и II и учитывая, что
u_к = 0, z₁= z₂, получим

.

Отсюда

. (4.18)

Для определения воспользуемся формулой гидростатического давления (см. § 3.7).

Применяя эту формулу для точек А и Д, получим

где 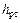- удельный вес ртути; h- удельный вес газа, скорость которого измеряется.

Так как при равновесии давление в точках А и Д одинаково, то

Учитывая, что 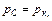получим

.

Подставляя последнее соотношение в (4.18), получим

Для каждой отдельной трубки вводится некоторый коэффициент , определяемый опытным путем. Отсюда формула для определения скорости потока принимает вид

§ 4.16. ТРУБКА ВЕНТУРИ, СОПЛО, ДИАФРАГМА

В промышленных условиях для измерения расхода жидкостей применяются трубки Вентури, сопла и диафрагмы. Более подробно рассмотрим трубку Вентури (рис. 4.25). Трубка Вентури создает в трубопроводе местное сужение потока и по возникающему перепаду давлений Dp можно определить расход жидкости.

Для сечений I и II запишем уравнение Бернулли (считая распределение скоростей равномерным)

,

где h_M - потеря напора между сечениями I и II, ; x - коэффициент местных потерь (см. § 6.21).

Уравнение неразрывности для несжимаемой жидкости имеет вид

.

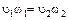Отсюда .

Подставляя h_M, u₁, и в уравнение Бернулли и выражая u₂, получим

.

Объемный расход будет определяться по формуле

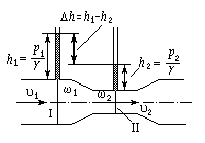Рис. 4.25

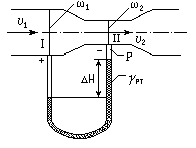Рис. 4.26

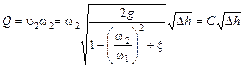, (4.19)

где C - величина, постоянная для данного расходомера (трубки Вентури).

Довольно часто вместо пьезометров 1 и 2 для измерения перепада давления в расходомере применяют дифференциальный трубный манометр
(рис. 4.26).

Рис. 4.27 Рис. 4.28

Учитывая, что над ртутью в трубках находится одна и та же жидкость плотностью r, можно записать (см. рис. 4.26)

. (4.20)

Значения , полученные по формуле (4.20), можно использовать для определения расхода по формуле (4.19).

Аналогично для измерения расхода могут быть использованы диафрагмы (рис. 4.27) и сопла (рис. 4.28).

Задача 1. При ламинарном режиме движения жидкости по горизонтальному трубопроводу диаметром расход жидкости равен (рис. 4.29). Падение пьезометрической высоты на участке длиной 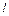составляет . Определить коэффициенты кинематической 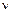и динамической вязкости жидкости. Исходные данные задачи:

; ; ; ; .

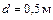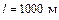Рис. 4.29

Решение.

; ; ; ;

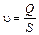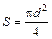. (а)

Запишем уравнение Бернулли для сечений 1 и 2 трубы

.

Так как и , то уравнение Бернулли примет вид

, где ; .

Учитывая, что 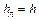, получим

.

Отсюда

.

Известно, что λ = 64/ Re – формула Пуазейля. Отсюда Re = 64/λ.

Подставляя последнее соотношение в (а), получим

.

Отсюда

.

Учитывая, что м², получим

.

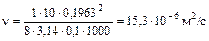Так как , то

.

Глава 5

ОСНОВЫ ТЕОРИИ ГИДРОДИНАМИЧЕСКОГО ПОДОБИЯ

Существует два метода исследования физических явлений – аналитический и экспериментальный. При аналитическом исследовании движения жидкости задача сводится к интегрированию сиcтемы дифференциальных уравнений при заданных условиях однозначности. Например, для вязкой несжимаемой жидкости имеем следующую сиcтему дифференциальных уравнений

; (5.1)

, (5.2)

где (5.1) – система уравнений Навье – Стокса, записанных в векторной форме (см. § 4.8); (5.2) - уравнение неразрывности. Кроме того, должны быть заданы начальные и граничные условия и значения физических постоянных r и n.

В принципе, совокупностью системы основных дифференциальных уравнений и условий однозначности конкретное единичное явление определено вполне. Однако эти уравнения чрезвычайно сложны (являются уравнениями в частных производных) и решения найдены лишь для небольшого числа частных случаев, к тому же при весьма существенных упрощающих предпосылках.

Другим методом исследования является непосредственный эксперимент. При этом измеряются те величины, которые представляют прямой практический интерес и находятся связи, допускающие непосредственное приложение. Однако данные, полученные из опыта, будут относиться только к тому частному случаю, который подвергался эксперименту. Необходимо найти пути обобщения данных опыта на другие родственные явления. Это позволило бы на основании немногих экспериментов судить о параметрах жидкости в многочисленных родственных явлениях. Задача нахождения научно обоснованного метода обобщения данных опыта решается теорией подобия, которая является учением о методах обобщения данных опыта.