
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Метод анализа размерности
Размерность какой-либо физической величины определяется соотношением между ней и теми физическими величинами, которые приняты за основные (первичные). В каждой системе единиц имеются свои основные единицы. Например, в Международной системе единиц измерения СИ за единицы измерения длины, массы и времени соответственно приняты метр (м), килограмм (кг), секунда (с). Размерность остальных физических величин, так называемых производных единиц (вторичных), принимается на основании законов, устанавливающих связь между этими единицами. Эта связь может быть представлена в виде так называемой формулы размерности.
Теория размерностей основана на двух положениях.
1. Отношение двух числовых значений какой-либо величины не зависит от выбора масштабов для основных единиц измерения (например отношение двух линейных размеров не зависит от того, в каких единицах они будут измеряться).
2. Любое соотношение между размерными величинами можно сформулировать как соотношение между безразмерными величинами. Это утверждение представляет так называемую П-теорему в теории размерности.
Из первого положения следует, что формулы размерности физических величин должны иметь вид степенных зависимостей
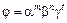 ,
,
где  - размерности основных единиц.
- размерности основных единиц.
Математическое выражение П-теоремы можно получить, исходя из следующих соображений. Пусть некоторая размерная величина а1 является функцией нескольких независимых между собой размерных величин а2, а3, а4,…, аn, т.е.
а1 = f (а2, а3, а4, …, аn).
Отсюда следует, что
j (а1, а2, а3, …, аn) = 0.
Допустим, что число основных размерных единиц, через которые могут быть выражены все n переменных величин, равно m. П-теорема устанавливает, что если все n переменные величины выразить через основные единицы, то их можно сгруппировать в n–m безразмерных членов П, т.е.
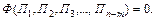
При этом каждый П-член будет содержать m+1 переменную величину.
В задачах гидромеханики число переменных, входящих в П-члены, должно равняться четырем. Три из них будут определяющими (обычно это характерная длина, скорость течения жидкости и ее плотность) - они входят в каждый из П-членов. Одна из этих переменных (четвертая) является различной при переходе от одного П-члена к другому. Показатели степени определяющих критериев (обозначим их через x, y, z) являются неизвестными. Показатель степени четвертой переменной для удобства примем равным – 1.
Соотношения для П-членов будут иметь вид
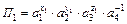 ;
;
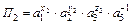 ;
;
. . . . . . . . . . . .
 .
.
Входящие в П-члены переменные можно выразить через основные размерности. Так как эти члены являются безразмерными, то показатели степени каждой из основных размерностей должны быть равны нулю. В результате для каждого из П-членов можно составить по три независимых уравнения (по одному для каждой размерности), которые связывают показатели степени входящих в них переменных. Решение полученной системы уравнений дает возможность найти числовые значения неизвестных показателей степени x, y, z. В итоге каждый из П-членов определяется в виде формулы, составленной из конкретных величин (параметров среды) в соответствующей степени.
В качестве конкретного примера найдем решение задачи определения потерь напора на трение при турбулентном течении жидкости [ 11 ].
Из общих соображений можно заключить, что потеря давления Dp в трубопроводе зависит от следующих основных факторов: диаметра d, длины l, шероховатости стенок k, плотности r и вязкости m среды, средней скорости течения u, начального напряжения сдвига t0, т.е.
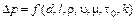
или
 . (5.8)
. (5.8)
Уравнение (5.8) содержит n = 7 членов, а число основных размерных единиц m = 3. Согласно П-теореме получим уравнение, состоящее из n–m = 4 безразмерных П-членов.
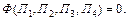
Каждый такой П-член содержит 4 переменные. Принимая в качестве основных переменных диаметр d, скорость u, плотность r и комбинируя их с остальными входящими в уравнение (5.7) переменными, получим
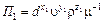 ;
;
 ;
;
 ;
;
 .
.
Составляя уравнение размерности для первого П-члена, будем иметь
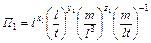 .
.
Складывая показатели степени при одинаковых основаниях, найдем
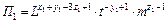 .
.
Для того чтобы размерность П1 была равна 1 (П1 – безразмерная величина), необходимо потребовать равенства нулю всех показателей степеней, т.е.
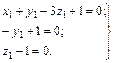 (5.9)
(5.9)
Система алгебраических уравнений (5.9) содержит три неизвестные величины x1, y1, z1. Из решения этой системы уравнений находим
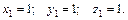
Подставляя эти значения показателей степени в первый П-член, получим
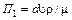 .
.
Аналогично для остальных П-членов будем иметь
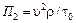 ;
;
 ;
;
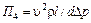 .
.
Подставляя полученные П-члены в (5.8), найдем
 .
.
Решим это уравнение относительно П4
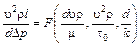 .
.
Выразим отсюда Dp
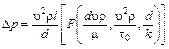 .
.
Учитывая, что потери напора на трение равны разности пьезометрических напоров, будем иметь
 .
.
Обозначив комплекс, находящийся в квадратных скобках, через 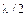 , окончательно получим
, окончательно получим
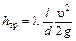 .
.
Последнее выражение представляет известную формулу Дарси-Вейбаха, где
 .
.
Формулы для расчета коэффициента трения l рассмотрены в § 6.18.
Глава 6
Классификация гидравлических потерь.
Режимы течения жидкости
Одной из важнейших задач гидравлики является определение потерь напора в трубопроводах. Знание этих потерь необходимо для расчета трубопроводов. Общую потерю напора на каком-либо участке трубопровода принято в гидравлике разделять на 2 вида потерь.
1. Потери напора по длине трубопровода или линейные потери напора.
2. Потери напора в местных сопротивлениях или местные потери напора.
Таким образом, потеря напора на участке 1-2 трубопровода определяется по формуле
h1-2 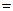 hл+ hм
hл+ hм
и измеряется в метрах столба (м ст.) жидкости.
Линейные потери напора - это потери напора на трение на прямых участках трубопровода. Потери напора по длине для трубопроводов, находящихся под напором, принято определять по формуле Дарси-Вейсбаха
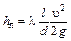 (в м ст.),
(в м ст.),
где l- длина участка трубопровода, м;
d- внутренний диаметр трубопровода, м;
l- коэффициент гидравлического сопротивления (коэффициент трения)- безразмерная величина.
Местные потери напора возникают в результате деформации потока и потерь энергии на вихреобразование в тех местах, где происходит изменение конфигурации канала. Они наблюдаются в местах поворота, резкого расширения или сужения потока, в различного рода запорных и регулирующих устройствах. Местные потери напора принято определять по формуле
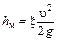 ,
,
где x - коэффициент местных потерь (безразмерная величина).
Таким образом, задача по определению гидравлических потерь при известной скорости течения среды сводится к нахождению коэффициентовl и x (теоретически или экспериментально).
Коэффициенты l и x обладают одним замечательным свойством: если потоки жидкости динамически подобны, то величина l или x для всех них будет иметь одно и то же значение, независимо от рода жидкости. Можно, например, получить l с опытами на воздухе и оно будет тем же и для воды и для масла и для любой другой жидкости, если число Re будет во всех этих случаях одно и то же. Это свойство легко объяснить с помощью теории подобия. Действительно,
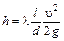 .
.
Так как 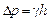 , то
, то
 .
.
Отсюда
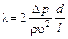
или
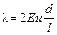 .
.
Для подобных потоков при Re = idem, 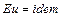 и
и  , поэтому и
, поэтому и 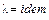 .
.
Аналогично из 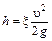 получим
получим
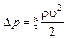 .
.
Отсюда
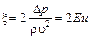 .
.
Дата добавления: 2015-04-18; просмотров: 275; Мы поможем в написании вашей работы!; Нарушение авторских прав |