ОСНОВНЫЕ ПОНЯТИЯ И ОПРЕДЕЛЕНИЯ ТЕОРИИ ПОДОБИЯ

Дадим некоторые определения теории подобия.

Под классом явлений понимается система дифференциальных уравнений, описывающих физическое явление. Например, системой уравнений Навье - Стокса и уравнением неразрывности описываются все возможные виды движения вязкой несжимаемой жидкости в каналах любой формы.

Под единичным явлением понимается система дифференциальных уравнений с наложенными на нее условиями однозначности. Действительно, если к системе дифференциальных уравнений присоединить условия однозначности и решить ее, то получим описание конкретного единичного явления.

Под группой явлений понимается система дифференциальных уравнений с наложенными на нее подобными условиями однозначности. Например, явления, протекающие в каналах, геометрически подобных, будут относиться к одной группе явлений.

Основная идея теории подобия заключается в выделении внутри класса явлений более узких групп.

Подобными явлениями называются такие, у которых отношение характеризующих их переменных есть постоянное число. Существуют следующие виды подобия.

1. Для того чтобы модель была механически подобна образцу (объекту, для которого создаётся модель), прежде всего должно соблюдаться геометрическое подобие; для этого отношение длин сходственных отрезков образца и модели должно быть одинаковым, т.е.

,

где l_м – некоторый линейный размер потока модели; l_о – соответствующий размер потока в образце; C_l – константа геометрического подобия (линейный масштаб модели).

Из последней формулы следуют также соотношения

; ,

где ω", ω' – площади модели и образца; V", V' – объёмы модели и образца.

2. При получении модели кроме геометрического подобия необходимо соблюдать ещё динамическое подобие, которое означает, что все силы, вызывающие рассматриваемые движения в модели, должны быть изменены с аналогичными силами в образце в одно и то же число раз.

Сила F определяется в виде произведения массы m на ускорение a, т.е.

.

Так как размерность массы m = ρl³, а ускорения a = l/t², то размерность силы будет

.

Отсюда следует, что для динамического подобия необходимо соблюдение соотношения

, (5.3)

где ; ;

C_f – константа динамического подобия (масштаб сил).

Условие (5.3) является математическим выражением общего закона динамического подобия, которое впервые сформулировано Ньютоном.

В теории подобия доказывается, что при выполнении геометрического и динамического подобия будет соблюдаться также и кинематическое подобие.

Следовательно, скорости, ускорения и перемещения частиц в модели будут изменяться в одних и тех же отношениях по сравнению с образцами, т.е.

; ; .

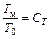Таким образом, для двух подобных явлений должны существовать соотношения типа

; ; ; и т.д.,

где C_{l ,} C_f , C_v , C_a сохраняют постоянные значения в соответственных точках подобных систем. Эти величины поэтому называются константами подобия.

Вообще говоря, подобных явлений бывает не два, а бесконечно большое количество. Эти явления составляют группу подобных явлений. Поэтому выражение вида есть групповое преобразование явлений, где C_x принимает последовательно постоянные значения при переходе от одного явления к другому, подобному первому.