Основное уравнение равномерного потока. Уравнение динамического равновесия равномерного потока

Проведем исследование равномерного потока с целью вывода основных уравнений, характеризующих его. При равномерном движении средние скорости во всех поперечных сечениях одинаковы, местные сопротивления отсутствуют и существуют лишь сопротивления трения, проявляющиеся по длине трубопровода и вызывающие соответствующие потери напора.

Выведем сначала уравнение динамического равновесия. Для этого рассмотрим равномерный поток жидкости в цилиндрической трубе (рис.6.5.).

Выделим в потоке отсек длиной l с площадью поперечного сечения w. Контур, ограничивающий площадку w, обозначим через c (хи). c обычно называют смоченным периметром. Контур c выберем концентрично по отношению к стенкам трубы.

На выделенный отсек действуют следующие силы.

1. Сила тяжести

G = γωl.

2. Силы гидродинамического давления

; ,

где p₁ и p₂- давления в соответствующих сечениях жидкости. (Поскольку в равномерном потоке гидромеханические давления распределяются в сечении по линейному закону, то в этих формулах под p₁ и p₂ cледует понимать давления, действующие в центре тяжести площадок w₁ и w₂ ).

Рис.6.5

3. Силы трения , где (cl) - боковая поверхность выделенного отсека.

Составим уравнение движения на направление l. Так как силы инерции в равномерном потоке отсутствуют, то получим

F₁ – F₂ – T + G sinβ = 0

или

.

Так как ,то

.

Поделив обе части уравнения на g и w и учитывая, что , находим

.

Обозначив , где R - гидравлический радиус, будем иметь

. (6.1)

Соотношение (6.1) представляет уравнение динамического равновесия равномерного потока.

Выведем уравнение энергии равномерного потока. Уравнение Бернулли для потока имеет вид

.

В равномерном потоке a₁ = a₂ и и, следовательно,

.

Тогда

. (6.2)

Объединяя (6.1) и (6.2), получим общее выражение для потери напора по длине потока

.

Последнее уравнение называют основным уравнением равномерного потока. Этому уравнению можно придать несколько иной вид

.

Отсюда

или

,

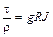где J - гидравлический уклон потока. Последние два соотношения также представляют основное уравнение равномерного потока.

Для касательного напряжения на стенке это уравнение принимает вид

или

.

Уравнение равномерного потока показывает, что напряжение силы трения, отнесенное к удельному весу жидкости, равно произведению гидравлического радиуса на гидравлический уклон.