Осреднение напряжений

За осредненное напряжение в данной точке принимается следующая величина

,

где T - время осреднения.

Аналогично для касательного напряжения .

Если произведено осреднение скорости, то действительную (истинную) скорость в данной точке можно представить как сумму средней скорости и величины отклонения скорости от средней в данный момент, т.е.

;

;

.

Величины получили названия пульсационных скоростей. Очевидно, , т.е. пульсационной скоростью называется разность между истинной скоростью в точке в данный момент и осредненной скоростью в этой же точке.

Пульсационные добавки напряжений будут определяться аналогичным образом

;

.

Заметим, что величина осредненной пульсационной добавки всегда равна нулю

; ; ,

что наглядно видно из графика пульсаций (см. рис.6.12).

Если измерять в некоторой точке скорости и давления жидкости, то при измерении обычными грубыми средствами - пьезометром, трубкой полного напора и т.п. практически не будут отмечаться пульсации. Скорости и давления нам будут представляться постоянными во времени .

По существу, будут измеряться осредненные во времени величины и . Кроме того, очевидно, что осредненное турбулентное движение в данном случае можно рассматривать как установившееся.

Рейнольдс предложил рассматривать не действительное движение жидкости, а осредненно-идеализированное. Этот осредненный поток в лучшей мере отвечает нашим опытным данным, относящимся, по существу, лишь к средним во времени величинам. Но тогда, как показал Рейнольдс, и дифференциальные уравнения должны содержать в качестве неизвестных не истинные переменные, а осредненные. В частности, Рейнольдс произвел осреднение уравнений Навье-Стокса, т.е. ввел вместо актуальных величин скоростей и давлений их осредненные значения.

При таком осреднении в уравнениях движения жидкости появляется 9 новых неизвестных членов типа .

То есть появляются какие-то новые силы (так как каждый член уравнения выражает силу).

Идеализация движения жидкости привела к идеализации и силовых соотношений. При этом замкнутая система уравнений Навье-Стокса оказалась разомкнутой. Появилась необходимость связать каким-то образом пульсации и c осредненными величинам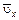и и и т.п. Эта связь может быть получена лишь на основании новых гипотез о механизме движения жидкости.

Так появились гипотезы турбулентности Маккавеева, Прандтля, Кармана, Тейлора, Фридмана и др. Но ни одна из этих гипотез ( за исключением гипотезы Фридмана) не в состоянии замкнуть систему уравнений. Они лишь сводят задачу к отысканию опытным путем каких-либо новых функций l,c и т.п., взамен пульсаций и . Эти функции могут быть легче определены из опыта, чем пульсации.

Подобные теории турбулентности названы полуэмпирическими, так как часть величин в них находится из опыта. Гипотеза же Фридмана, хотя и замыкает систему уравнений, но сводит ее к системе из 20-ти дифференциальных уравнений в частных производных весьма сложного вида. Поэтому практически эта гипотеза использована быть не может.

Мы рассмотрим лишь наиболее простые случаи осредненных потоков и лишь наиболее распространенную полуэмпирическую теорию турбулентности Прандтля (см. § 6.15).