Логарифмический закон распределения скоростей в круглой трубе

На рис. 6.17 даны эпюры скорости ламинарного (1) и турбулентного (2) потоков при одинаковых расходах в круглой цилиндрической трубе. В ламинарном гидродинамическом пограничном слое турбулентного потока (d_л ) имеет место линейный закон изменения скорости, а в турбулентном ядре
(d_т ) – логарифмический закон. В ламинарном потоке закон изменения скорости параболический.

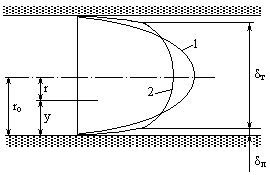
Рис. 6.17

Выведем закон распределения скорости в круглой трубе для турбулентного потока вблизи стенки, за исключением ламинарного пограничного слоя (d_л ). При турбулентном движении инерционное касательное напряжение определяется по формуле (пренебрегая напряжением от молекулярной вязкости)

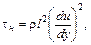
где l – длина пути перемешивания при переходе жидкости из одного слоя в

другой.

Примем следующие допущения:

1) касательное напряжение по всему поперечному сечению потока одинаково и равно касательному напряжению на стенке ;

2) длина пути перемешивания пропорциональна расстоянию от стенки

,

где c - коэффициент пропорциональности, определяемый из опыта.

С учетом принятых допущений формула для t_н примет вид

или

.

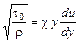Известно, что

,

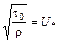где 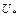- динамическая скорость.

Тогда

.

Отсюда

.

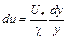Интегрируя, получим

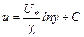. (6.14)

Следовательно, в области турбулентного потока около стенки скорость изменяется по логарифмическому закону (кривая 2 на рис. 6.17).

Опытом установлено, что при соответствующем выборе постоянной c эта формула может быть распространена на все живое сечение трубы, за исключением ламинарного слоя, где скорость изменяется по линейному закону.

Так как формулу (6.14) можно распространить на все живое сечение трубы, то определим постоянную C из того условия, что при , .

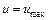Тогда

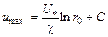. (6.15)

Вычитая из (6.15) выражение (6.14), получим

.

Или, переходя к десятичным логарифмам 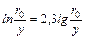и подставляя c=0,4 (для гладких труб), получим

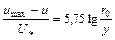. (6.16)

Разность называется дефицитом скорости, а выражение в левой части - относительным дефицитом. Таким образом, относительный дефицит скорости является функцией только безразмерного расстояния .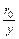

Установим соотношение между средней и максимальной скоростью. Пусть при некотором значении y_ср скорость жидкости равна средней скорости u_ср.

Тогда можно записать

.

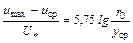Вследствие того что относительный дефицит скорости есть всегда одна и та же функция 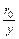, то и средняя ордината должна пересекать кривую

всегда в одной и той же точке с абсциссой , т.е. должно быть

.

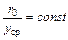Cледовательно,

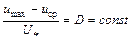. (6.17)

Расчеты и эксперимент показывают, что можно принять

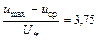. (6.18)

Формулы (6.16) и (6.18) позволяют производить построение эпюр скоростей в турбулентном ядре потока.