Местные сопротивления

При движении реальных жидкостей кроме потерь на трение по длине потока, возникающих из-за вязкости жидкости, могут возникать и местные потери напора. Причиной последних являются местные сопротивления (краны, задвижки, сужения, расширения, повороты трубопроводов, и прочее), которые вызывают изменение скорости движения или направления потока.

Потери напора в местных сопротивлениях определяются по формуле

, (6.20)

где x - коэффициент местных потерь;

- cкоростной напор;

u - средняя скорость.

Коэффициентом местных потерь x называется отношение потери напора в данном местном сопротивлении к скоростному напору

.

Очень часто диаметр трубопровода до местного сопротивления и после него бывает разным, а поэтому и скорости потока при этом разные (рис.6.21). Очевидно, что и коэффициенты местных потерь, отнесенные к скоростному напору до и после местного сопротивления, будут различными. Поэтому при пользовании гидравлическими справочниками необходимо всегда обращать внимание, к какому скоростному напору отнесен коэффициент x. Обычно x относят к скоростному напору за местным сопротивлением.

В некоторых случаях удобно определять местные сопротивления через так называемую эквивалентную длину местного сопротивления. Эквивалентная длина местного сопротивления - это такая длина прямого трубопровода, на которой происходит такая же потеря напора h_м, как и в данном местном сопротивлении.

Эквивалентную длину l_э можно определить из равенства

.

Отсюда

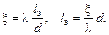
Понятие эквивалентной длины позволяет ввести понятие о приведенной длине трубопровода

где l - действительная длина трубопровода.

Коэффициент местных потерь x в общем случае зависит от формы местного сопротивления, от числа Re, от шероховатости поверхности, а для запорных устройств также от степени их открытия, т.е.

,

где симплексы характеризуют форму местного сопротивления, в том числе и степень открытия в случае запорного устройства.

Ввиду большой сложности происходящих в местных сопротивлениях явлений в настоящее время нет надежных методов теоретического определения коэффициента x. Он определяется в основном экспериментально. Имеется попытка теоретически обосновать коэффициент местных потерь на случай внезапного расширения трубопровода (рис. 6.22). Используя аналогию потерь энергии при внезапном расширении с неупругим ударом твердых тел, Борда из теоремы о приращении количества движения и уравнения Бернулли вывел формулу для местных потерь при внезапном расширении потока в виде

где u₁, u₂ - скорости потока до и после внезапного расширения. Т.е. потеря напора при внезапном расширении равна скоростному напору потерянной скорости, где u = u₁– u₂ – потерянная скорость. Это утверждение представляет так называемую теорему Борда-Карно. Однако более детальный анализ явлений показывает, что аналогия потерь напора при внезапном расширении с потерями энергии при неупругом ударе твердых тел далеко неполная. Опытом, в частности, подтверждается, что потери напора, даваемые теоремой Борда-Карно, получаются завышенными. Поэтому на основании теоретических соображений и эксперимента предложено эту потерю определять по формуле

, (6.21)

где k - коэффициент, определяемый опытным путем.

Ценность такого теоретического обоснования коэффициента x , когда вместо него нужно из опыта находить коэффициент k, очевидна.

Рассмотрим теперь отдельные практически важные типы местных сопротивлений.

1. Внезапное расширение потока (см. рис. 6.22).

Хотя аналогия внезапного расширения потока с неупругим ударом не может служить основой для строгого теоретического обоснования и объяснения физического смысла явления, в первом приближении она достаточна. Благодаря неупругости удара механическая энергия рассеивается и превращается во внутреннюю энергию жидкости. Этим и объясняется основная доля потерь при внезапном расширении, которые подсчитываются по формуле (6.21).

Уравнение неразрывности потока для несжимаемой жидкости имеет вид

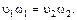(6.22)

Отсюда

. (6.23)

Подставляя (6.23) в (6.21), получим

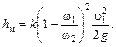(6.24)

Сравнивая (6.24) с (6.20), найдём

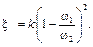(6.25)

Выразим из (6.22) u₁

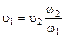. (6.26)

Подставляя (6.26) в (6.21), получим

(6.27)

Сравнивая (6.27) с (6.20), найдём

.

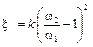Таким образом, по формулам (6.24), (6.27) можно определить потери напора в местном сопротивлении в случае известных скоростей u₁ или u₂. Для приближенных расчётов коэффициент k можно принять равным 1.

Рис. 6.23	Рис. 6.24

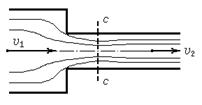
2. Выход из трубы в резервуар больших размеров (рис. 6.23).

В данном случае площадь сечения резервуара ω₂ >> ω₁ и поэтому

.

Тогда из формулы (6.25) следует

» 1.

3. Внезапное сужение потока (рис. 6.24).

В данном случае происходит внезапное увеличение скорости. Удара при этом в плоскости перехода сечения не происходит. Но на некотором расстоянии ниже по течению происходит сжатие струи (сечение с–с), а затем переход от сжатого сечения к нормальному. Этот переход можно рассматривать как удар, что и служит причиной потерь напора.

Потери напора при внезапном сужении значительно меньше потерь напора при внезапном расширении. Коэффициент ξ здесь зависит от соотношения ω₂ / ω₁. Найденные опытным путём значения ξ приведены в таблице

4. Постепенное расширение потока (диффузор) (рис. 6.25).

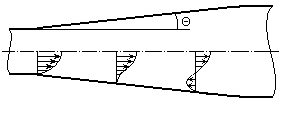
Рис. 6.25

При малых углах q £ 4-5⁰. Течение в диффузоре происходит безотрывно. При углах q > 4-5⁰ происходит отрыв потока от стенки. Это объясняется тем, что в диффузоре происходит увеличение давления в направлении движения, вызываемое уменьшением скорости вследствие расширения канала. Частицы жидкости, движущейся у стенки, сильно затормаживаются силами вязкости и в определенной точке их кинетическая энергия становится недостаточной для преодоления все возрастающего давления. Поэтому скорость жидкости в пристенном слое в такой точке обращается в нуль, а за этой точкой появляются обратные течения - отрыв потока.

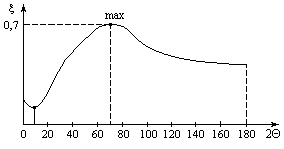
Рис. 6.26

Если безотрывное течение в диффузоре происходит практически без потерь, то течение с отрывом сопровождается значительными потерями энергии на вихреобразование.

Зависимость 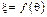имеет вид, представленный на рис. 6.26.

При угле 2q @ 70⁰ коэффициент потерь достигает максимума. Причем, при угле 2q > 40⁰¸60⁰ потери напора превосходят потери при внезапном расширении потока (2q = 180⁰). Поэтому вместо переходов в виде диффузоров с углом 2q > 40⁰ нужно применять внезапное расширение как переход, дающий меньшие потери напора.