
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Основные расчетные формулы для определения потерь напора
Линейные потери напора в напорных трубопроводах круглого сечения определяются по формуле Дарси-Вейсбаха
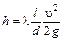 ,
,
где u - средняя по сечению скорость.
Эта формула называется первой водопроводной формулой. Из нее следует
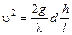
или
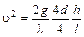 . (6.30)
. (6.30)
Так как  ;
;  , где R - гидравлический радиус; J - пьезометрический (гидравлический) уклон, то (6.30) примет вид
, где R - гидравлический радиус; J - пьезометрический (гидравлический) уклон, то (6.30) примет вид
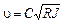 , (6.31)
, (6.31)
где  - коэффициент Шези.
- коэффициент Шези.
Формула (6.31) называется формулой Шези. Она используется для определения скорости течения при равномерном движении жидкости в трубах, каналах и естественных руслах. Коэффициент C может быть вычислен, если известно l, или его определяют по эмпирическим формулам, например, по эмпирической формуле Павловского
 ,
,
где n - коэффициент шероховатости (дается в таблицах);  - переменный показатель степени, равный
- переменный показатель степени, равный
 .
.
Из формулы Шези найдем
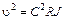
или
 .
.
Отсюда
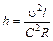 .
.
По этой формуле находятся линейные потери напора, главным образом при расчете некруглых труб.
Местные потери напора рассчитываются по общей формуле
 .
.
С целью упрощения гидравлических расчетов формулу Шези представляют в несколько ином виде. Учитывая, что
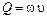 ,
,
получим

или
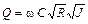 .
.
Обозначив
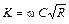 ,
,
получим

или
 .
.
Отсюда
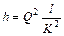 .
.
Последняя формула называется второй водопроводной формулой.
Величина K называется модулем расхода или расходной характеристикой. При 
 , т.е. K представляет собой расход жидкости в трубопроводе при гидравлическом уклоне, равном единице. Следовательно, K имеет размерность расхода. С другой стороны, при
, т.е. K представляет собой расход жидкости в трубопроводе при гидравлическом уклоне, равном единице. Следовательно, K имеет размерность расхода. С другой стороны, при  из 2-й водопроводной формулы получаем
из 2-й водопроводной формулы получаем  , т.е.
, т.е. 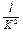 представляет собой сопротивление трубопровода при расходе, равном единице. Поэтому величину
представляет собой сопротивление трубопровода при расходе, равном единице. Поэтому величину 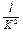 называют удельным сопротивлением трубопровода.
называют удельным сопротивлением трубопровода.
Особенно удобно введение величины K при расчете трубопроводов с турбулентным движением в квадратичной зоне. В этом случае
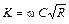 .
.
Часто 2-й водопроводной формуле придают другой вид. Так как
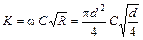 ,
,
то
 .
.
Обозначив
 ,
,
получим
 .
.
Тогда из формулы

получим еще один вид второй водопроводной формулы
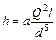 .
.
Задачи
Задача 1. По трубопроводу (рис. 6.29) диаметром 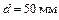 и длиной
и длиной 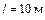 движется жидкость (керосин). Определить напор
движется жидкость (керосин). Определить напор 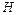 , при котором происходит смена ламинарного режима течения на турбулентный (потери напора в местных сопротивлениях не учитывать). Температура жидкости
, при котором происходит смена ламинарного режима течения на турбулентный (потери напора в местных сопротивлениях не учитывать). Температура жидкости 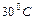 . Кинематический коэффициент вязкости керосина
. Кинематический коэффициент вязкости керосина 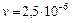 м2/с.
м2/с.
Рис. 6.29
Решение. Считая, что в данном случае смена ламинарного режима течения на турбулентное происходит при числе Рейнольдса, равном 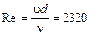 , линейные потери напора будут определяться по формуле Дарси - Вейсбаха
, линейные потери напора будут определяться по формуле Дарси - Вейсбаха
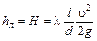 ,
,
где 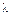 - коэффициент линейных потерь;
- коэффициент линейных потерь;  - ускорение свободного падения;
- ускорение свободного падения; 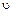 - скорость течения жидкости, которая может быть определена из числа Рейнольдса
- скорость течения жидкости, которая может быть определена из числа Рейнольдса
 .
.
Коэффициент линейных потерь находится по формуле Пуазейля
 .
.
Искомый напор 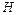 затрачивается лишь на преодоление линейных потерь напора, поэтому он может быть найден по формуле Дарси-Вейсбаха
затрачивается лишь на преодоление линейных потерь напора, поэтому он может быть найден по формуле Дарси-Вейсбаха
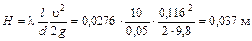 .
.
Задача 2.Определить диаметр  трубопровода, по которому подается жидкость Ж с расходом
трубопровода, по которому подается жидкость Ж с расходом  , из условия получения в нем максимально возможной скорости при сохранении ламинарного режима при следующих исходных данных:
, из условия получения в нем максимально возможной скорости при сохранении ламинарного режима при следующих исходных данных: 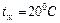 ;
; 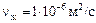 ;
; 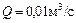 .
.
Решение. Расход, скорость и число Рейнольдса определяются по формулам
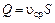 ;
; 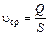 ;
; 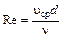 .
.
Максимальная скорость, при которой сохраняется ламинарный режим течения, будет наблюдаться при числе Рейнольдса, равном  . Тогда
. Тогда
 .
.
Отсюда
 м.
м.
Задача 3.По трубопроводу диаметром  и длиной
и длиной 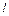 (рис. 6.30) движется жидкость (вода, ν = 1·10-6 м2/с). Определить потерю напора
(рис. 6.30) движется жидкость (вода, ν = 1·10-6 м2/с). Определить потерю напора  , при которой происходит смена ламинарного режима течения на турбулентный. Исходные данные задачи:
, при которой происходит смена ламинарного режима течения на турбулентный. Исходные данные задачи:  ;
; 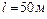 .
.
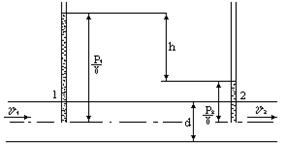
Рис. 6.30
Решение.Потеря напора определяется по формуле Дарси – Вейсбаха
 .
.
Коэффициент линейных потерь находится по формуле Пуазейля
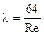 ,
,
где  .
.
Тогда
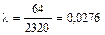 .
.
Скорость 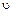 найдем из числа Рейнольдса
найдем из числа Рейнольдса
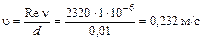 .
.
Тогда
 м.
м.
Задача 4.При внезапном расширении трубопровода скорость жидкости в трубе большего диаметра равна 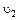 (рис. 6.31). Большой и малый диаметры трубы соответственно равны
(рис. 6.31). Большой и малый диаметры трубы соответственно равны 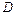 и
и  . Причем,
. Причем, 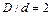 . Определить разность показаний пьезометров
. Определить разность показаний пьезометров  , при следующих исходных данных:
, при следующих исходных данных:
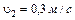 ;
; 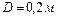 ;
; 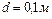 .
.

Рис. 6.31
Решение.Из уравнения неразрывности потока имеем
 . (а)
. (а)
Так как  ;
; 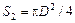 ;
;  , то
, то 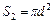 .
.
Потеря напора при внезапном расширении трубопровода находится по формуле
 .
.
Из соотношения (а) находим
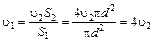 .
.
Отсюда
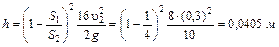 .
.
Дата добавления: 2015-04-18; просмотров: 639; Мы поможем в написании вашей работы!; Нарушение авторских прав |