Экспериментальные данные для коэффициента гидравлического сопротивления. Опыты Никурадзе и Зегжда

При исследовании турбулентного движения жидкости в трубах необходимо решать два основных вопроса – определение потерь напора и распределения скоростей по поперечному сечению трубы. Опыты показывают, что обе эти величины существенно изменяются в зависимости от диаметра трубы, вязкости жидкости, скорости движения и шероховатости стенок труб.

Экспериментальные данные для l в широком интервале чисел Re были получены Никурадзе в трубах и Зегжда - в прямоугольных каналах с искусственной (песочной) шероховатостью.

Средний диаметр фракции песка D принимался за меру абсолютной шероховатости (рис.6.18). Труба называется гидравлически гладкой, если средняя высота выступов шероховатости D меньше толщины ламинарной пленки d_л. В этом случае шероховатость не влияет на движение. Если абсолютная шероховатость D больше толщины ламинарной пленки d_л, то труба называется гидравлически шероховатой. В этом случае шероховатость существенно влияет на движение жидкости (рис.6.19).

Рис.6.19

Таким образом, абсолютная шероховатость D это есть средняя высота выступов шероховатости. Относительная шероховатость определяется величиной

,

где r₀ - радиус трубы.

Величина, обратная относительной шероховатости

,

называется относительной гладкостью.

Результаты опытов Никурадзе представлены на графиках рис.6.20.

Рис.6.20

На графике (см. рис.6.20) всю область чисел Рейнольдса можно разделить на 5 характерных зон движения.

1 - зона ламинарного режима (Re < 2300 или lgRe < 3,6). Здесь все опытные точки, независимо от шероховатости стенок, ложатся на прямую линию I, описываемую уравнением Пуазейля

.

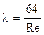Следовательно, опытные данные позволяют заключить, что при ламинарном движении шероховатость стенок не оказывает влияние на сопротивление (коэффициент трения). Потери напора здесь пропорциональны скорости. Действительно, подставляя выражение для коэффициента трения

в формулу Дарси-Вейсбаха

,

получим

,

где u - средняя скорость,

.

2 – переходная зона. В ней ламинарный режим переходит в турбулентный (2300 ≤ Re ≤ 3000). Коэффициент λ здесь быстро возрастает с увеличением числа Рейнольдса, оставаясь одинаковым для различных шероховатостей.

3 - зона гидравлически гладких труб для турбулентного режима. Для труб с высокими значениями относительной гладкости (r₀/D>500). Опытные точки для чисел Рейнольдса 400<Re<80 r₀/D располагаются вдоль наклонной прямой II. Эта прямая известна как прямая Блазиуса для «гладких труб». На ней коэффициент трения l хорошо описывается эмпирической формулой Блазиуса

.

Потери напора здесь определяются по формуле

.

4 - зона шероховатых труб (r₀/D<500) или, так называемая, доквадратичная зона при турбулентном режиме (80 r₀/D<Re< 1000r₀/D). В этой зоне отклонение экспериментальных точек от прямой II зависит от величины шероховатости (относительной гладкости). И это отклонение наступает тем раньше, чем меньше относительная гладкость. При этом коэффициент l стремится к некоторому пределу (разному для труб с различной шероховатостью), оставаясь затем постоянным при увеличении числа Re.

5 - зона вполне шероховатых труб (r₀/D=15 и r₀/D=30). Гидравлические потери в этой области пропорциональны квадрату скорости (квадратичный закон сопротивления). Для кривых r_o/D=15 и r_o/D=30 ламинарная пленка даже при небольших значениях Re не перекрывает выступов шероховатости и эти кривые с увеличением числа Re только пересекают линию II для гладких труб. Следовательно, в данном случае коэффициент l совершенно на подчиняется закону для гладких труб. С увеличением числа Re он постепенно возрастает и при lg Re = 4,6 для первой кривой (r_o/D=15) или lg Re =5,0 для второй кривой (r_o/D=30) становится практически независимым от Re.

Коэффициент l для этой зоны может быть определен по формуле
Б.Л. Шифринсона

,

где D_э – эквивалентная шероховатость (см. ниже).

Полученным результатам можно дать следующее объяснение. До тех пор, пока выступы шероховатости полностью погружены в ламинарный пограничный слой (D< d_л), для величины гидравлических сопротивлений нет разницы между гладкими и шероховатыми поверхностями стенок. Коэффициент l здесь зависит только от числа Рейнольдса и определяется как для гладких труб (1-3-я зоны).

В случае, когда выступы шероховатости выходят за пределы пограничного слоя (D>d_л), ламинарное течение нарушается и выступы шероховатости оказываются в области турбулентного течения жидкости.

С увеличением числа Рейнольдса толщина пограничного слоя уменьшается и в случае, когда величина D оказывается сопоставимой с величиной d_л, коэффициент l зависит не только от числа Рейнольдса, но и от шероховатости стенок (4-я зона).

Если число Рейнольдса достаточно велико и D значительно больше d_л, то коэффициент l зависит только от шероховатости и не зависит от числа
Рейнольдса (5-я зона).

Опыты А.П.Зегжда для прямоугольных каналов позволили получить график, который близок к графику Никурадзе не только качественно, но и количественно, если результаты сопоставлять при одинаковых гидравлических радиусах.

Опыты, проведенные в промышленных трубопроводах с естественной шероховатостью, показали, что оценка только по высоте выступов шероховатости D недостаточна, большую роль имеет также характер шероховатости: форма выступов, их расположение и прочее. Поэтому было введено понятие об эквивалентной шероховатости D_э= φD (φ > 1), где φ - зависит от характера шероховатости. Под эквивалентной шероховатостью D_э понимают такую зернистую шероховатость, при которой сопротивление оказывается таким же, как и при действительной шероховатости. Величина эквивалентной шероховатости D_э указывается в гидравлических справочниках в зависимости от типа трубопровода.