Гидравлический расчет простого трубопровода

Исходными выражениями для расчета трубопровода являются.

1. Уравнение Бернулли .

2. Водопроводные формулы ; .

3. Формула для определения местных потерь напора .

Рассмотрим установившееся движение жидкости по трубопроводу, соединяющему два резервуара A и B (из сосуда A жидкость переливается в сосуд B (рис. 7.2)).

Рис. 7.2

Составим уравнение Бернулли для сечений I и II.

,

где Σh = h_л + h_м – сумма линейных и местных потерь напора.

Так как u₁ = u₂ @ 0, а также , то

.

Отсюда следует, что разность геометрических напоров полностью идет на покрытие потерь.

Формула для суммарной потери напора имеет вид

,

где - коэффициент сопротивления системы.

Тогда

.

Отсюда

и

.

В том случае, когда местными потерями можно пренебречь и при турбулентном режиме движения, расход можно определить непосредственно по формуле

,

где K - модуль расхода (см.§ 6.22).

Составляя уравнение Бернулли для сечений a и b, убеждаемся, что разность пьезометрических напоров идет на преодоление сопротивления по длине

.

Без учета местных сопротивлений линия полного напора будет выражаться прямой линией с постоянным наклоном (линия АВ на рис.7.2).

Если трубопровод состоит из ряда отдельных участков с различными диаметрами, последовательно соединенных между собой (рис. 7.3), то задача решается аналогично

,

где .

Формула для в развернутом виде будет

или

.

Рис. 7.3

При неучете местных потерь и турбулентном движении

.

Учитывая, что

,

получим

.

Для простого трубопровода . Тогда

.

Отсюда

.

Последнюю формулу можно записать в виде

, (7.1)

где –

коэффициент пропускной способности трубопровода.

Формулу (7.1) перепишем в виде

,

где 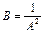- коэффициент гидравлической характеристики трубопровода.

Рассмотрим теперь как в случае простого трубопровода решаются упомянутые выше три частные задачи.

1. Заданы расход Q и размеры трубопровода (диаметр d и длина l). Определить перепад напора DH.

Из уравнения Бернулли

,

определив среднюю скорость

,

находим

или

.

2. Заданы перепад напоров DH и размеры трубопровода (диаметр d и длина l). Определить расход Q.

Определив среднюю скорость

,

найдем

или

.

3. Заданы расход Q и перепад напоров DH. Определить диаметр трубопровода d (длина и конфигурация трубопровода также считаются заданными).

В простейшем случае, когда местными сопротивлениями можно пренебречь,

.

Так как

,

то

.

Отсюда

.

Для квадратичной области можно принять , если шероховатость трубопровода задана, и, следовательно, d определено явно.

Если и, следовательно, , так как , то расчет усложняется и ведется методом последовательных приближений.

Для ламинарного режима

и

.

Так как

,

то

.

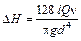Отсюда

.

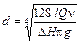Имеются и другие методы решения этой задачи.