Решение задачи об оптимальном выборе потребителя.

Кривые безразличия графически отражают систему предпочтений потребителя. Естественно, потребитель стремится приобрести товарный набор, принадлежащий наиболее удаленной от начала координат кривой безразличия. Однако, это не всегда возможно, т.к. выбор набора ограничивается средствами, которыми располагает потребитель.

Обозначим рыночные цены блага X через Р_х, цены блага Y через P_y, доход потребителя через I; тогда бюджетное ограничение потребителя можно записать в виде уравнения:

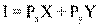. (5.8)

т.е. доход потребителя равен сумме его расходов на покупку товаров X и Y.

Преобразуем уравнение (5.8) и получим уравнение бюджетной линии (5.9), которая имеет вид прямой линии (рисунок 5.6). Чем выше доход, тем дальше от начала координат находится линия бюджетного ограничения.

. (5.9)

Рис. 5.6 Бюджетная линия

Пусть задана линия бюджетного ограничения и несколько кривых безразличия. В рамках бюджетного ограничения потребитель постарается так распределить свой доход между различными благами, чтобы максимизировать полезность U. Соответствующий набор благ называется оптимальным планом потребления и обычно обозначается точкой касания бюджетной линии и кривой безразличия.

Рис. 5.7 Оптимальный выбор потребителя

Для ситуации, представленной на рисунке 5.7, оптимум потребителя будет в точке С.

В точке оптимума соотношение цены блага X к цене блага Y равно предельной норме замещения блага X благом Y, т.е. выполняется равенство:

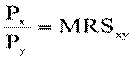(5.10)

Во многих прикладных исследованиях важную роль играет коэффициент эластичности. Под эластичностью понимают меру реагирования эндогенной (зависимой) переменной на изменение экзогенной (независимой) переменной.

Приведем также более конкретное определение: эластичность - предел соотношения между относительным приращением функции y (зависимой переменной) и относительным приращением независимой переменной x когда и обозначается E_x(y).

Таким образом, эластичность можно выразить формулой:

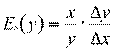при (5.11)

или в непрерывном случае:

. (5.12)

На практике эластичность относят к проценту прироста независимой переменной. Тогда эластичность показывает, на сколько процентов повышается или понижается эндогенная переменная Y, если независимая переменная X изменяется на 1%.

Различают дуговую эластичность, то есть среднюю на каком-то отрезке кривой, и точечную эластичность - значение производной в заданной точке. Для практического вычисления эластичности используется формула английского математика и экономиста Рой Аллена (1906­1983). Он предложил использовать среднюю точку интервала, по которому происходит изменение, в качестве знаменателя дроби. Тогда вычисляются:

относительное изменение эндогенной переменной: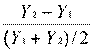

и относительное изменение экзогенной переменной:

.

Затем вычисляется отношение первого ко второму.

Формула Аллена имеет широкое распространение, однако ее не следует применять к очень широким интервалам, поскольку в этом случае она может ввести в заблуждение.

Для определения эластичности спроса от цены можно воспользоваться формулой:

при (5.13)

Коэффициент эластичности спроса по цене показывает, на сколько процентов уменьшится (увеличится) спрос, если цена товара увеличится (уменьшится) на 1%.

И, наконец, существуют различные степени эластичности спроса по цене. Так, спрос неэластичен по цене, если спрос на товар практически не зависит от его цены, в этом случае коэффициент эластичности близок к нулю. Примером товаров с неэластичным спросом являются предметы первой необходимости. Спрос нормально эластичен, если E_d.p ≈ 1, что имеет место для товаров длительного пользования. Спрос является суперэластичным для предметов роскоши E_d.p > 1.