
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Моделирование процесса достижения рыночного равновесия
Равновесная цена в конкурентной экономике без сговора достигается в результате стихийного процесса: при любой цене, превышающей равновесную, количество товара, которое стремятся предложить продавцы (производители), будет превосходить то количество, на которое покупатели (потребители) намерены предъявить спрос; в результате возникает давление на цену в сторону ее понижения. Аналогично цена, находящаяся ниже уровня равновесия, испытывает давление в сторону повышения.
По А. Маршаллу различают мгновенное, кратковременное и длительное рыночное равновесие в зависимости от цены, т.е. наличии не меняющейся во времени функции спроса D(p).
Мгновенное равновесие достигается в обстановке, когда предложение фиксировано (  ), т.е. производители товара не готовы к расширению производства или не в состоянии это сделать; равновесие такого рода обычно достигается при достаточно высокой цене
), т.е. производители товара не готовы к расширению производства или не в состоянии это сделать; равновесие такого рода обычно достигается при достаточно высокой цене  , что и является стимулом для последующих действий производителей.
, что и является стимулом для последующих действий производителей.
Кратковременное равновесие возникает тогда, когда в действие вводятся наличные резервы (свободные производственные мощности) и предложение несколько увеличивается, причем  ; равновесная цена
; равновесная цена  в этой ситуации оказывается ниже
в этой ситуации оказывается ниже  , но и остается еще довольно высокой.
, но и остается еще довольно высокой.
Длительное нормальное равновесие устанавливается в ситуации, когда в деле принимают участие практически все производители, способные производить данный товар без резкой перестройки своей хозяйственной деятельности. Функция предложения 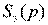 также возрастающая и равновесная цена
также возрастающая и равновесная цена  соответствует нормальным издержкам производства.
соответствует нормальным издержкам производства.
Процесс приближения к нормальному равновесию во времени можно представить при помощи последовательности малых дискретных шагов; при этом функции спроса и предложения сами могут изменяться в ходе указанного процесса вследствие изменения условий производства и потребления.




















Рис. 5.12 Длительное нормальное равновесие на рынке
Рассмотрим паутинообразную модель процесса достижения рыночного равновесия.
В процессе моделирования используется дискретное представление процесса с помощью так называемых “торговых” дней с номерами 
Предполагается, что к началу торгового дня t известна начальная цена товара 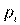 , которая полностью определяет объем предложения
, которая полностью определяет объем предложения
 . (5.15)
. (5.15)
Далее считается, что в течение дня предложенный товар полностью реализуется по цене  , которая определяется из условия временного равновесия
, которая определяется из условия временного равновесия  (5.16)
(5.16)
и является исходной ценой для следующего торгового дня (t+1) и т.д.
Геометрическая иллюстрация этого процесса приближения к равновесию (рис.5.13) напоминает паутину и поэтому сама модель часто называется паутинообразной. Можно показать, что сходимость указанного рыночного процесса будет гарантирована, если выполнено условие
 . (5.17)
. (5.17)























Рис. 5.13 Паутинообразная модель
Последнее означает, что для сходимости достаточно, чтобы маргинальное предложение не превосходило бы маргинального спроса, или, иными словами, положительная реакция производителя на повышение цены не была бы столь же значительной как отрицательная реакция потребителя, т.е. это процесс в обстановке относительно неактивных производителей. Заметим, что если  , то возникает ситуация так называемого “свиного цикла”, при которой состояние равновесия оказывается недостижимым. В случае, если наклон линии спроса круче наклона линии предложения, спираль будет раскручиваться в обратном порядке. Если наклоны линий спроса и предложения одинаковы, то паутина закольцуется (Рис. 5.14):
, то возникает ситуация так называемого “свиного цикла”, при которой состояние равновесия оказывается недостижимым. В случае, если наклон линии спроса круче наклона линии предложения, спираль будет раскручиваться в обратном порядке. Если наклоны линий спроса и предложения одинаковы, то паутина закольцуется (Рис. 5.14):

Рис. 5.14 Закольцованная паутинообразная модель
(равновесие на рынке недостижимо)
Рассмотрим ситуацию наличия активных производителей, готовых сразу же откликнуться на возникающий спрос. В этом случае процесс задается при помощи следующей системы соотношений:
- в торговый день t задано предложение  и оно определяет цену
и оно определяет цену 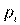 как решение уравнения (5.18):
как решение уравнения (5.18):
 . (5.18)
. (5.18)
- эта цена характеризует объем спроса:
 (5.19)
(5.19)
- а предложение на следующий торговый день прямо ориентируется на спрос предыдущего дня:
 (5.20)
(5.20)
Описанный процесс также может быть представлен при помощи паутинообразной модели, причем достаточное условие сходимости имеет вид:  что соответствует более сильной реакции производителей по сравнению с потребителями.
что соответствует более сильной реакции производителей по сравнению с потребителями.
Рассмотрим процесс достижения равновесия на следующем примере.
Пусть функция предложения S(p) = 4p - 3,
а функция спроса 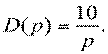
Основное соотношение имеет вид:

Отсюда цена в каждый следующий рыночный день определяется через цену в предыдущий день по формуле:
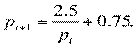
Предположим, что начальная цена  , и сведем результаты расчета в таблицу 5.1.:
, и сведем результаты расчета в таблицу 5.1.:
Сходимость цены к равновесной во времени Таблица 5.1
| p | D | S | Δ =D-S |
| 1,5 | 6,67 | 3,67 | |
| 2,42 | 4,14 | 6,67 | -2,53 |
| 1,78 | 5,61 | 4,14 | 1,47 |
| 2,15 | 4,65 | 5,61 | -0,96 |
| 1,91 | 5,23 | 4,65 | 0,58 |
| 2,06 | 4,85 | 5,23 | -0,38 |
| 1,96 | 5,10 | 4,85 | 0,25 |
| 2,02 | 4,95 | 5,10 | -0,15 |
| 1,99 | 5,02 | 4,95 | 0,07 |
| 2,01 | 4,98 | 5,02 | -0,04 |
| 2,00 | 4,98 | 0,02 |
Таким образом, мы видим, что по прошествии 11 “рыночных” дней процесс установления цены сходится к состоянию равновесия, причем получается уже известное нам значение равновесной цены . Заметим, что промежуточные значения цены попеременно становятся то больше, то меньше равновесной величины. Это означает, что процесс имеет колебательный характер с уменьшающейся амплитудой (см. рис. 5.15).

Рис.5.15 Процесс сходимости цены к равновесной.
ЛИТЕРАТУРА
1. Основная
1. Дорохина Е.Ю., Халиков М. А. Моделирование микроэкономики. ─М.: ЭКЗАМЕН, 2003.
2. Экономико-метематические методы и модели. Под ред. проф. А.В. Кузнецова. ─ Минск: БГЭУ, 2000.
3. Экономико-математические методы и прикладные модели / под ред. Федосеева В.В. – М.: ЮНИТИ, 1999.
4. Шелобаев С.И. Математические методы и модели в экономике, финансах, бизнесе. Учебное пособие для ВУЗов. ─ М.: ЮНИТИ-ДАНА, 2000.
5. Экономико-математическое моделирование. Под ред. проф. И.Н.Дрогобыцкого. Учебник. ФИНАНСОВАЯ АКАДЕМИЯ ПРИ ПРАВИТЕЛЬСТВЕ РФ. – М.:ЭКЗАМЕН, 2004.
6. Федосеев В.В., Эриашвили Н.Д. Экономико-математические методы и модели в маркетинге. Учебное пособие для ВУЗов. / Под ред. В.В. Федосеева. ─ М.:
7. Шелобаев С. И. Экономико-математические методы и модели. Второе издание. ─ М.: ЮНИТИ, 2005.
1. Дополнительная
1. Абчук В.А. Экономико-математические методы. ─СПб: Союз, 1999.
2. Багриновский К.А., Матюшок В.М. Экономико-математические методы и модели (микроэкономика). – М.: Изд-во Российского университета дружбы народов, 1999.
3. Большаков А.С. Моделирование в менеджменте. Учебное пособие. - М.: Филинъ, 2000.
2. Горчаков А.А., Орлова И.В. Компьютерные экономико-математические модели. – М.: «Компьютер» Изд-во ЮНИТИ, 1995.
3. Замков О.О., Черемных Ю.А., Толстопятенко А.В. Математические методы в экономике. Под общей ред. Сидоровича А.В. 2-ое издание. – М.: Дело и сервис, 1999.
4. Ильченко А.Н. Экономико-математические методы. М.: Финансы и статистика, 2006.
5. Лопатников Л.И. Экономико-математический словарь 4-е издание – М.: Наука, 1996.
6. Монахов А. В. Математические методы анализа экономики. Учебное пособие. СПб.: ПИТЕР, 2002.
7. Малыхин В.И. Математика в экономике. Учебное пособие. ─ М.: ИНФРА-М, 2001.
8. Орлова И.В. Экономико-математические методы и модели. Выполнение расчетов в вреде Excel / Практикум. Учебное пособие для ВУЗов. - М.: Финстатинформ, 2000.
9. Тарасевич В.М. Экономико-математические методы и модели в ценообразовании. В 2-х частях – Л.: ЛФЭИ, 1991 .
10. Томас Р. Количественные методы анализа хозяйственной деятельности / пер. с англ. - М.: Дело и сервис, 1999.
11. Хайман Д.Н. Современная микроэкономика: анализ и применение. В 2-х томах. Пер. с англ. – М.: Финансы и статистика, 1992.
12. Шрайбер Т.Дж. Моделирование на GPSS. Пер. с англ. Под ред Файнберга. – М.: Машиностроение, 1980.
13. Эддоус М., Стэнннсфилд Р. Методы принятия решений / Пер. с англ. под ред. член-корр. РАН И.И.Елисеевой. – М.: Аудит, ЮНИТИ, 1997.
[1] Гранберг А.Г. Моделирование социалистической экономики. – М.: Экономика, 1988.
Дата добавления: 2014-11-13; просмотров: 358; Мы поможем в написании вашей работы!; Нарушение авторских прав |