Анализ полезности товаров, кривые безразличия.

В качестве основных факторов потребительского выбора рассматриваются полезность товара, цена на товар, доход покупателя. Существуют два основных подхода к анализу полезности как основного фактора потребительского выбора – количественный и порядковый.

Количественный подход к анализу полезности основан на представлении о возможности измерения полезности различных благ в гипотетических единицах - ютилах (utility-полезность). Количественная функция общей полезности (TU) вначале возрастающая, имеет точку максимума (S), после которой она становится убывающей (см. рис.5.1).

Предельная полезность (MU) показывает прирост общей полезности товарного набора при увеличении объема потребления данного товара на единицу и рассчитывается по следующей формуле:

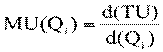(5.1)

Чаще всего, как видно на рисунке 5.1, предельная полезность падает и в точке максимума становится равной нулю, а далее - отрицательной.

TU

S

QA

MU

QA

Рис. 5.1 График функции общей (TU) и предельной (MU) полезности.

Порядковый подход к анализу полезности является более распространенным и исходит из того, что человеку присущи отношения предпочтения при оценке им полезности тех или иных товаров.

Рассмотрим основную предпосылку теории оптимального выбора потребителя: потребитель осуществляет право сравнения и свободного выбора на некотором множестве X потребительских наборов, в каждый из которых включаются все виды продукции, которые являются предметами потребления для данной группы семей (потребителей). Можно считать, что всякий такой набор состоит из фиксированного числа ( n ) элементов и имеет вид:

Х = (x1, . . . , xj, . . . , xn) ,

где элементы x_j ≥ 0 , поскольку они выражают количество потребляемой продукции.

Далее предполагается, что сравнительная оценка различных наборов данным потребителем с точки зрения его вкусов, привычек, традиций и т.д., может быть выражена при помощи т.н. бинарного отношения слабого предпочтения.

Это отношение определено на множестве потребительских наборов X , выражается формулой “предпочтительнее чем ...или равноценен”, записывается при помощи знака “=”.

Формула “x=y” , где x и y суть потребительские наборы означает, что данный потребитель (группа семей) в равных условиях либо предпочтет набор x набору y, либо не видит различия между ними, т.е. считает их равноценными.

На базе отношения слабого предпочтения вводится отношение безразличия (равноценности): два набора x и y безразличны для потребителя, если одновременно выполняются условия “x=y” и “y=x”. Факт равноценности двух наборов обычно записывается при помощи выражение “y ~ x”. Понятие строгого (сильного) предпочтения определяется следующим образом: “x y” тогда и только тогда, когда “x=y”, а соотношение “y= x” не имеет места.

Рассмотрим наборы только из двух товаров Χ и Υ. (Товары Χ и Υ можно рассматривать как комбинированные товары). Отношения предпочтения, характерные для каждого индивида, отражают посредством кривой безразличия, изображенной на рисунке 5.2.

Кривая безразличия отражает множество точек, каждая из которых представляет собой такой набор из двух товаров, что потребителю безразлично (равноценно), какой из этих наборов выбрать.

Наборы А и В с точки зрения данного потребления равноценны и лежат на одной и той же кривой безразличия I. Для нашего потребителя любой набор, лежащий на кривой II, предпочтительнее любого набора, лежащего на кривой I и т. д.

Рис. 5.2 Кривые безразличия

Предельная норма замещения (MRS - marginal rate of substitution) - основное рабочее понятие порядковой теории полезности.

Предельной нормой замещения блага X благом Y (MRSxy) называют количество блага Y, которое должно быть сокращено «в обмен» на увеличение количества блага X на единицу, с тем чтобы уровень удовлетворения потребителя остался неизменным:

при условии, что U= const (5.2)

Выделяют следующие типы кривых безразличия в зависимости от функций полезности: кривые безразличия линейного типа; неоклассического типа; кривые безразличия функций с полным взаимодополнением благ.

Кривые безразличия линейного типа соответствуют функции полезности с полным взаимозамещением благ (чай и кофе), которая имеет следующий вид:

(5.3)

где - параметры;

- полезность;

- товары.

Из функции полезности (5.3) можно найти Y:

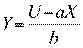(5.4)

и построить кривые безразличия линейного типа (см. рис. 5.3):

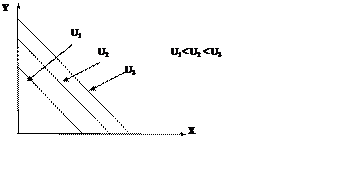
Рис. 5.3 Кривые безразличия линейного типа

Неоклассическая функция полезности имеет вид:

, где . (5.5)

Чтобы построить кривые безразличия необходимо найти Y:

(5.6)

Рис.5.4 Кривые безразличия неоклассического типа

Функции с полным взаимодополнением благ имеют кривые безразличия в виде точки на пересечении двух прямых. При этом полные взаимодополнение благ предполагает, что при увеличении спроса на одно из двух благ растет спрос и на второе благо, например, сахар и чай, бензин и моторное масло. Избыток одного блага не имеет значения, полезность достигается лишь при определенной комбинации обоих благ:

(5.7)

Рис. 5.5 Кривые безразличия функций с полным взаимодополнением благ