
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Решение одноэтапной целочисленной задачи методом коэффициента интенсивности.
Введение в модель задачи РРП нелинейности и дискретности (целочисленности) значительно затрудняет решение. Универсальных методов решения таких задач не существует, но часто используется приближенный метод «коэффициентов интенсивности».
Метод «коэффициентов интенсивности» основан на замене однократного решения нелинейной задачи развития и размещения производства с дискретными переменными многократным решением последовательности обычных линейных транспортных задач с дискретными переменными. Переход от одной транспортной задачи к другой осуществляется взаимосвязанным изменением мощности и соответствующих ей удельных производственных затрат для какого-либо одного пункта производства.
Таким образом, решение задачи состоит из последовательности этапов. На первом этапе решается открытая транспортная задача с неизвестными  .
.
Ограничение (4.55) на этом этапе выглядит так:
 (4.56)
(4.56)
где  максимально возможная мощность в i-м пункте строительства.
максимально возможная мощность в i-м пункте строительства.
*После распределения поставок по потребителям производится проверка целочисленности решения. Для этого для каждого i-го пункта строительства рассчитывается коэффициент интенсивности.
Коэффициент интенсивности (  ) представляет дробь, в числителе которой сумма поставок реальным потребителям, а в знаменателе производственная мощность поставщика на данном этапе:
) представляет дробь, в числителе которой сумма поставок реальным потребителям, а в знаменателе производственная мощность поставщика на данном этапе:
 (4.57)
(4.57)
По результатам расчета коэффициент интенсивности  может принимать следующие значения:
может принимать следующие значения:
 если
если  соответствующий вариант мощности отвергается полностью;
соответствующий вариант мощности отвергается полностью;
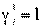 если
если  данный вариант мощности поставщика может быть включен в оптимальный план развития и размещения;
данный вариант мощности поставщика может быть включен в оптимальный план развития и размещения;
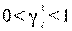 если
если  смешанная строка, мощность поставщика используется не полностью, только часть продукции, произведенной в i-м пункте по k- му проекту, распределяется между реальными потребителями, часть продукции закрепляется за фиктивным потребителем.
смешанная строка, мощность поставщика используется не полностью, только часть продукции, произведенной в i-м пункте по k- му проекту, распределяется между реальными потребителями, часть продукции закрепляется за фиктивным потребителем.
Задача будет решена, если для всех строк  будут равны 1 или 0.
будут равны 1 или 0.
При наличии смешанной строки, что свидетельствует о нецелочисленном решении, осуществляется переход к следующему этапу. Для этого из всех смешанных строк выбирается та, которой соответствует минимальное значение  . Поставщика с минимальным
. Поставщика с минимальным  называют переходным, и при переходе к следующему этапу только у этого производителя меняется мощность на ближайшее меньшее значение, что ведет к увеличению удельных затрат, а значит к уменьшению конкурентоспособности этого производителя. Решается новая транспортная задача, после чего процесс повторяется, начиная с позиции, помеченной звездочкой*.
называют переходным, и при переходе к следующему этапу только у этого производителя меняется мощность на ближайшее меньшее значение, что ведет к увеличению удельных затрат, а значит к уменьшению конкурентоспособности этого производителя. Решается новая транспортная задача, после чего процесс повторяется, начиная с позиции, помеченной звездочкой*.
Расчеты повторяют до получения целочисленного решения, т.е. на каком-то s-ом этапе моделирования ограничение (4.56) принимает вид
 где
где  (4.58)
(4.58)
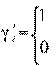 (4.59)
(4.59)
что означает: каждый из вариантов строительства либо используется в полном объеме, либо не используется совсем.
Пример 4.4. Пусть новые предприятия по производству одинакового продукта могут быть построены в четырех пунктах А,Б,С,Д. а их продукция может поставляться в четыре пункта потребления (I, II, III и IV). Варианты мощностей предприятий и соответствующие им удельные производственные затраты представлении в табл. 4.8, а потребности и удельные транспортные затраты в табл. 4.9:
Таблица 4.8
| Предприятие | Варианты мощности (т) | Удельные приведенные затраты, (тыс.руб/т). |
| А | ||
| В | ||
| С | ||
| Д |
Таблица 4.9
| Поставщики | I | II | III | IV |
| A | ||||
| B | ||||
| C | ||||
| D |
Мощности в каждом пункте производства могут принимать лишь отдельные дискретные значения, поэтому зависимость удельных производственных затрат от размеров мощности задана не в виде функции, а в табличном виде.
Требуется определить оптимальную мощность промышленных предприятий в пунктах строительства и рациональную схему прикрепления поставщиков к потребителям, которые обеспечивает минимум затрат.
На первом этапе данного метода в каждом пункте производства принимаются максимальные проектные мощности . Соответствующие им удельные производственные затраты построчно суммируются с транспортными. Получается схема обычной транспортной задачи (см. Табл. 4.10):
Таблица 4.10
| Мощность постав-щика | Потребители и их спрос | Фиктивный потребитель | ||||
| I - 600 | II- 400 | III - 400 | 1V – 200 | |||
| А - 400 | - | |||||
| B - 600 | 400 | 0,33 | ||||
| C - 600 | _ | |||||
| D - 600 | 200 | 0,67 |
Решаем открытую транспортную задачу: закрепляем потребителей за поставщиками по «методу наименьших стоимостей». Для этого выбираем клетку с наименьшими затратами и заполняем ее объемом поставок - в соответствии со спросом потребителей и мощностью поставщика. Далее переходим к следующей незаполненной клетке с наименьшими затратами и заполняем таким образом всю таблицу. При этом ставится задача полного обеспечения спроса каждого из потребителей. Мощности поставщиков могут быть задействованы не полностью; неиспользуемые реальными поставками мощности проставляем в колонке «фиктивный потребитель».
Далее переходим к проверке условия целочисленности. Для этого по каждому i-му пункту строительства рассчитывается коэффициент интенсивности как отношение суммы реальных поставок к мощности, взятой на данном этапе.
Из таблицы 4.10 видно, что минимальный коэффициент интенсивности 0,33 соответствует поставщику В. Переходим к новому этапу решения задачи, изменив для строительства в пункте В мощность с 600 на 500 тонн (по данным табл. 4.8) и, соответственно, суммарные удельные затраты от этого поставщика.
Таблица 4.11
| Пункты строительства | потребители | |||||
| I-600 | II-400 | III-400 | IV–200 | Фиктивный потребитель | ||
| А - 400 | -- | |||||
| -- | ||||||
| В - 500 | -- | -- | ||||
| С - 600 | -- | |||||
| -- | ||||||
| D - 600 | -- | |||||
| -- |
После решения второго этапа (см. таблицу 4.11) все коэффициенты интенсивности равны 0 или 1, это значит, что решение окончательное, найдено оптимальное решение: план размещения и развития включает строительство предприятий в трех пунктах: пункт А (предприятие мощностью 400 т), пункт С (предприятие мощностью 600 т), пункт Д (предприятие мощностью 600 т).
Доставка продукции будет производиться по следующим направлениям:
• из пункта А второму потребителю в объеме400 т (X12=400);
• из пункта С первому потребителю в объеме 600 т (X 31=600);
• из пункта Д третьему потребителю в объеме 400 т (X43 =400);
четвертому потребителю в объеме 200 т (X44=200).
Общая стоимость затрат на производство и доставку продукции составит 292 млн. руб.
 .
.
Дата добавления: 2014-11-13; просмотров: 390; Мы поможем в написании вашей работы!; Нарушение авторских прав |