Основные положения оптимизации размещения крупных производств в регионах.

Оптимальным вариантом развития и размещения производств (РРП) является такой вариант строительства новых, реконструкции и расширения существующих хозяйственных объектов который бы обеспечил удовлетворение спроса на продукцию и эффективное развитие производства.

В качестве критерия оптимальности в большинстве задач выступают минимум затрат на заданный объем конечного продукта, или максимум прибыли, или максимум производства высокоэффективной продукции отрасли.

Варианты РРП, оптимальные с точки зрения выбранного критерия, должны включать описание следующих условий:

- спрос на продукцию и другие условия реализации;

- возможность использования дефицитных ресурсов (ограничения по ресурсам);

- устоявшиеся взаимосвязи между отдельными хозяйствующими объектами;

- транспортные условия по доставке сырья, материалов, готовой продукции и т.д.

- социальные, экологические и другие внешние условия.

Экономико-математические модели данных задач формируются для определенного отрезка времени, поэтому здесь уместна динамическая постановка задачи. Поскольку в реализации динамических задач имеется ряд трудностей методического и информационного характера, чаще рассматривается упрощенная статическая модель. Экономические показатели, используемые при расчетах, учитывают изменение во времени оценок ресурсов и продукции, для этого используются коэффициенты дисконтирования.

Классификация РРП задач может производится по нескольким признакам:

1. В зависимости от способа задания варианта развития и размещения:

- в безвариантной постановке,

- в вариантной постановке.

2. В зависимости от характера переменной

- с непрерывными переменными,

- с дискретными переменными.

3. По степени влияния транспортного фактора:

- транспортно – производственные задачи,

- производственные задачи.

4. По числу позиций номенклатуры выпускаемой продукции:

- однопродуктовые,

- многопродуктовые.

5. По степени возможной локализации системы:

- одноэтапные (поставщик – потребитель),

- многоэтапные (поставщик – изготовитель (переработчик) – потребитель).

Простейшие модели РРП относятся к отраслям, производящим один вид продукции в количестве, достаточном для удовлетворения спроса потребителей. Задача может быть сведена к обычной транспортной задаче, т.е. к закреплению потребителей за поставщиками, которое обеспечивает минимум транспортных затрат. Модель простой транспортной задачи, рассмотренная в разделе 2.3, являлась закрытой, однопродуктовой, транспортно-производственной (одноэтапной), безвариантной.

Однако задача отраслевого размещения усложняется в условиях, когда мощности поставщиков не удовлетворяют спрос потребителей. Это требует ввода новых мощностей путем строительства новых промышленных предприятий, путем расширения, реконструкции действующих.

Введем следующие обозначения:

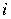– индекс пункта производства (строительства, реконструкции) ;

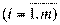– индекс пункта потребления ;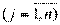

a_i – верхний предел мощности в i–м пункте производства (строительства, реконструкции);

b_j – спрос j -го потребителя на продукцию отрасли;

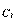– затраты на производство единицы продукции в i-м пункте нового строительства (расширения, реконструкции действующего предприятия);

t_ij – транспортные расходы по перевозке продукции от i-го пункта строительства к j-тому пункту потребления,

x_ij – объем поставок продукции от i-го пункта производства к j-му пункту потребления,

x_i –размер производства в i-ом пункте.

Требуется определить значения величин x_ij и x_i , минимизирующих суммарный объем затрат на производство и доставку продукции

(4.47)

при выполнении следующих ограничений:

• суммарный ввоз продукции в каждый из пунктов потребления должен быть равен его потребностям

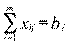(j=1,n), (4.48)

• Суммарный вывоз продукции из каждого пункта производства должен быть равен размеру производства, а последний не может быть больше предельного значения

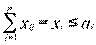
, (4.49)

• объемы перевозок по всем направлениям и размеры производства в каждом из пунктов производства должны быть неотрицательны

(4.50)

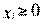
Результат решения задачи по алгоритму транспортной задачи дает оптимальную схему транспортных связей и оптимальный вариант размещения производства. Причем решение дает ограничение типа (4.49) , из которого следует: в пунктах, которые в оптимальном распределении окажутся связанными с реальными потребителями, целесообразно развивать производство в размере: .

С учетом условия (4.49) критерий оптимальности (4.47) можно переписать:

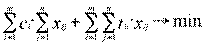(4.51)

или после преобразований

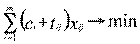(4.52)

В этой модели принято, что величина производственных затрат пропорциональна объемам производства. Однако экономическая теория и практика свидетельствуют, что величина производственных затрат существенно зависит от объемов производства продукции, т.е. являются функцией от них. Концентрация производства приводит к снижению удельных производственных затрат вследствие экономии, например, на накладных расходах, вследствие чего общую величину производственных затрат надо определять как произведение переменного норматива, представляющего собой функцию от размеров производства, на объем производства (нелинейная зависимость). Поэтому решение модели данной задачи можно использовать только для предварительных (эскизных) расчетов на начальных этапах исследования.