
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Использование статической модели межотраслевого баланса в прогнозировании цен.
Использование информации о межотраслевых взаимосвязяхпозволяет, в частности, отслеживать - в какой мере изменение цен на продукцию одной отрасли повлияет на изменение цен на продукцию других отраслей.
Согласно упрощенному подходу индекс цен на продукцию j-той потребляющей отрасли в зависимости от изменения цен на продукцию i-той производящей отрасли определяется по следующей формуле:
 , (4.23)
, (4.23)
где Pi и Pj - соответственно, индексы цен на продукцию i-той производящей и j-той потребляющей отраслей.
Пусть речь идет о двух отраслях: пищевой (n=2) и энергетической (n=1). Как изменение цен на энергоресурсы при прочих неизменных условиях отразится на росте цен на продукцию пищевой промышленности?
Согласно (4.23) можно записать:

Недостатком данной формулы является рассмотрение только прямых затрат электроэнергии на производство продукции пищевой промышленности, при этом косвенные затраты не рассматриваются. Но для производства продукции пищевой промышленности в технологическом процессе используется продукция сельского хозяйства, на производство которой тоже необходима электроэнергия. Эти косвенные затраты не учитываются в формуле (4.23).
Использование модели МОБ позволяет учитывать полные затраты электроэнергии в производстве и дать более точный прогноз изменения цены продукции пищевой промышленности.
Обоснуем формулу, позволяющую увязать изменение индексов цен в различных отраслях. В качестве основы используем уравнение взаимосвязи I и III квадрантов МОБ (4.2):
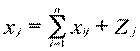
Прогноз цен на период t производится на основе данных МОБ предыдущего периода (t-1).
Пусть в результате инфляции в прогнозном периоде предполагается рост цен, который характеризуется индексом роста цен в i-той отрасли Pi. При этом структура затрат в сопоставимых ценах не изменилась, а индекс роста всех элементов условно-чистой продукции j-той отрасли совпадает с индексом роста цен в этой же отрасли.
В таблице 4.3 показано, как изменение цены в i-ой отрасли отразилось на содержании схемы МОБ :
Таблица 4.3
Схема первого и третьего квадрантов МОБ в текущих ценах
| Отрасли производители | Отрасли потребители | |||
| … | n | |||
| . . n | x11p1 x21p2 . . xn1pn | x12p1 x22p2 . . xn2pn | … … … … … | x1np1 x2np2 . . xnnpn |
| Чистая продукция отрасли | z1 | z2 | … | zn |
Тогда уравнение (4.2) запишется так:
 (4.24)
(4.24)
разделим обе части на Xj

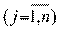 (4.25)
(4.25)
Уравнения (4.24) и (4.25) позволяют производить расчеты по влиянию изменения цен продукции i-ых отраслей на изменение цен по всей совокупности отраслей народного хозяйства.
Пример 4.2. Пусть данные о структуре затрат отчетного периода представлены в таблице 4.4.
Таблица 4.4
Содержание первого и третьего квадрантов трехотраслевого МОБ
| Отрасли производители | Отрасли потребители | ||
| 984,4 227,1 37,9 | 173,7 86,9 37,2 | 59,1 136,3 48,3 | |
| Добавленная (вновь созданная) стоимость в отрасли | 643,6 | 1023,2 | 293,3 |
| Валовая продукция |
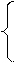 Предположим, что цена продукции в первой отрасли выросла в 10 раз, что привело к увеличению цен на продукцию других отраслей в р2 и р3 раза соответственно при той же структуре затрат. Поскольку задан индекс цен на продукцию первой отрасли, считается, что величина затрат на продукцию первой отрасли не влияет на формирование цены в этой отрасли. Система (4.24) будет состоять из двух балансовых уравнений для второй и третьей отраслей:
Предположим, что цена продукции в первой отрасли выросла в 10 раз, что привело к увеличению цен на продукцию других отраслей в р2 и р3 раза соответственно при той же структуре затрат. Поскольку задан индекс цен на продукцию первой отрасли, считается, что величина затрат на продукцию первой отрасли не влияет на формирование цены в этой отрасли. Система (4.24) будет состоять из двух балансовых уравнений для второй и третьей отраслей:

После приведения подобных и решения системы получается решение:
Р2 = 10,2; р3 = 11,3.
Таким образом, повышение цен на продукцию первой отрасли в 10 раз приведет к повышению цен на продукцию второй отрасли в 10,2 раза, и третьей отрасли в 11,3 раза (при условии, что индекс роста всех элементов добавленной стоимости совпадает с индексом роста цен).
Как правило, индекс роста заработной платы отстает от роста цен. Так, в 1995 году коэффициент эластичности заработной платы от цен составил 0,75. Это условие может быть отражено в предыдущей модели. В третьем квадранте в составе вновь созданной стоимости выделим заработную плату:
1 2 3
| Добавленная (вновь созданная) стоимость в отрасли | Заработная плата | 377,1 | 351,9 | 75,4 |
| Остальные элементы | 266,5 | 671,3 | 217,9 |
 Тогда модель (4.21) должна быть записана в виде:
Тогда модель (4.21) должна быть записана в виде:

Уравнение (4.24) может быть использовано также для обоснования последствий изменения отдельных элементов условно-чистой продукции (амортизации, косвенных налогов, прибыли).
Дата добавления: 2014-11-13; просмотров: 739; Мы поможем в написании вашей работы!; Нарушение авторских прав |