Экономико-математическая модель межотраслевого баланса.

Расчеты межотраслевого баланса на основе уравнений (4.4) производить трудно из-за сложности информационного обеспечения элементов промежуточного потребления . Поэтому расчеты основываются на системе нормативов расходов факторов производства. В составе этой системы важное место занимают коэффициенты прямых и полных затрат материальных ресурсов (коэффициенты прямых и полных материальных затрат).

Введем понятие «Коэффициент прямых материальных затрат» а_ij, который показывает, какое количество продукции i-той отрасли непосредственно необходимо, если учитывать только прямые затраты, для производства единицы продукции j -ой отрасли. Значение а_ij не зависит от объемов производства в j-ой отрасли и является довольно стабильной величиной во времени, отражая сложившиеся нормы затрат на производство единицы продукции j-ой отрасли. Они могут быть выражены в натуральной или стоимостной форме.

Коэффициенты прямых затрат а_ij рассчитываются по формуле

i, j =1,2,…., n (4.9)

отсюда следует

(4.10)

Подставляя выражение (4.10) в систему уравнений баланса (4.4) получим:

(4.11)

Выражение (4.11) представляет статическую модель МОБ в виде системы уравнений. Это модель «затраты ­ выпуск», предложенная В.Леонтьевым.

Модель МОБ можно представить в компактной (векторной форме).

Положим А ­ матрица коэффициентов прямых материальных затрат (технологическая матрица):

Вектор ­ столбец валовой продукции Хи вектор ­ столбец конечной продукции Y:

Система уравнений (4.11) в матричной форме примет вид:

. (4.12)

Выражение (4.12) представляет матричную форму модели межотраслевого баланса.

С помощью этих моделей можно решать три варианта задач:

1) известны величины валовой продукции каждой отрасли , определить объем конечной продукции каждой отрасли .

Введем единичную матрицу размерности (n x n), диагональные элементы которой равны единице, а остальные ­ нулю.

Тогда на основе (4.12) можно записать:

(4.13),

это уравнение (4.13) позволяет решить задачу первого типа.

2) Известны величины конечной продукции всех отраслей , требуется определить величины валовой продукции каждой отрасли . Из (4.13) получим:

, (4.14)

где ­ матрица, обратная матрице .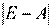

4. Для ряда отраслей известны значения валовой продукции, а для всех остальных отраслей заданы объемы конечной продукции. Требуется найти величины конечной продукции первых отраслей и объемы валовой продукции вторых отраслей. Для решения этой задачи удобнее пользоваться не матричной формой модели МОБ, а системой линейных уравнений (4.4).

Введем понятие коэффициентов полных материальных затрат, для этого обозначим новую матрицу:

, (4.15)

Тогда систему уравнений в матричной форме (4.14) можно записать в виде:

. (4.16)

Элементы матрицы обозначим , тогда из матричного уравнения (4.16) для любой отрасли можно получить следующее соотношение:

, i = 1,2, …,n. (4.17)

Коэффициенты называются коэффициентами полных материальных затрат, а матрица , определяемая как , называется матрицей коэффициентов полных материальных затрат.

Чтобы пояснить экономический смысл коэффициентов полных затрат , перепишем (4.15) в развернутом виде (как результат перемножения матрицы на вектор ):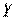

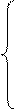
(4.18)

Предположим, что осуществляется выпуск конечной продукции только одной (например, первой отрасли) в размере 1млрд руб., т.е.

Подставляя значения конечной продукции в систему (4.18), получим, что для того, чтобы обеспечить конечную продукцию первой отрасли в указанном объеме необходимо обеспечить валовой выпуск продукции остальных отраслей соответственно в объеме , , …., . Таким образом, элементы первого столбца матрицы показывают количество валовой продукции всех отраслей, необходимых для производства единицы конечной продукции первой отрасли. Аналогично можно показать, что элементы j-го столбца матрицы показывают количество валовой продукции отраслей, необходимых для производства единицы конечной продукции j-ой отрасли. Другими словами, каждый из коэффициентов полных материальных затрат показывает, сколько всего нужно произвести продукции i-ой отраслью для выпуска в сферу конечного использования единицы продукции j-ой отрасли.

В отличие от коэффициентов прямых затрат а_ij , коэффициенты полных материальных затрат включают в себя как прямые затраты (затраты, возникающие непосредственно при изготовлении данной продукции), так и косвенные затраты (затраты в предшествующие стадии производства, отраженные в средствах производства).

Дата добавления: 2014-11-13; просмотров: 34; Нарушение авторских прав