Простая однономенклатурная статическая модель управления запасами.

Рассмотрим модель простой системы управления запасами на примере склада. Эффективность работы склада оценивается по его затратам на пополнение запасов и их хранение. Работа реального склада сопровождается множеством отклонений от идеального режима, но для составления простейшей однопродуктовой статической модели управления запасами делаются следующие предположения:

- скорость расходования запасов со склада (спрос) является постоянной величиной, обозначим ее v (единиц товарных запасов в единицу времени),

- объем поступающей партии qявляется постоянной величиной,

- интервал времени между двумя поставки τ (цикл) является постоянным,

дефицит недопустим,

- запас пополняется мгновенно от 0 до величины .

Динамика изменения уровня запаса на складе имеет вид, представленный на рис.3.17:

Рис. 3.17 График пополнения запаса идеального склада.

Обоснуем формулу для определения оптимального размера партии заказа, который обеспечивает минимум затрат.

Введем обозначения:

К ­ затраты, не зависящие от объема партии,

S ­ затраты на хранение одной единицы запасов в течение одной единицы времени.

Издержки хранения запасов будем считать пропорциональными величине хранящихся запасов и времени их хранения. Величина среднего размера запасов за время τ равна .

Таким образом, суммарные затраты за время τ при размере партии равны:

(3.34)

Учитывая, что 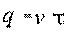, величина затрат на пополнение и хранение запасов в единицу времени равна:

(3.35)

Это выражение является целевой функцией, минимизация которой позволяет определить оптимальные режим работы склада. Так, оптимальный размер партии, при котором обеспечивается минимум затрат на пополнение и хранение запаса, можно определить методами дифференциального исчисления:

,

откуда оптимальный размер партии:

. (3.36)

Эта формула называется формулой Уилсона по имени английского ученого­экономиста, который ее вывел в 20-х годах XX столетия.

Используя формулу Уилсона можно определить ряд расчетных характеристик работы идеального склада в оптимальном режиме:

оптимальная периодичность пополнения запасов

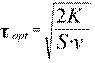, (3.37)

минимальные суммарные затраты на управление запасами в единицу времени

. (3.38)

Пример 3.12Растительное масло разливается по бутылкам на линии разлива и упаковки. Затраты на организацию поставок масла составляют 700 ден.ед., спрос на масло 140 тыс. литров в месяц, стоимость хранения 1 литра в течение месяца ­ 4 ден.ед. Определить оптимальные параметры системы. Сравнить рассчитанные оптимальные затраты с затратами по действующей системе разлива партии в течение 3-х дней.

Исходные данные: К=700 ден.ед, =140000 л., S=4 ден.ед., =3 дня.

Расчет оптимальных параметров:

• оптимальный размер партии

литров,

• оптимальная длительность цикла

мес. = 1,5 (дня),

• затраты на поставку и хранение

ден.ед. (в месяц).

Фактические показатели работы:

• цикл поставки составляет 3 дня или 0,1 месяца,

• размер партии литра,

• затраты за месяц составляют (из формулы 3.34)

ден. ед.

Сравнивая рассчитанные оптимальные показатели работы системы с их фактическими значениями, можно сделать следующий вывод. Если установить цикл поставки в 1,5 дня (вместо 3-х дней), а размер партии поставки сделать равным 7000 литрам (вместо фактических 14000 литров), можно снизить издержки функционирования системы с 35000 ден. ед. до 28000 ден. ед. в месяц.