Основные зависимости для линейной производственной функции.

Рассмотрим использование факторов производства, при котором возможно как компенсация уменьшения затрат одного фактора увеличением другого, так и полное замещение одного фактора производства другим. Производственный процесс, который удовлетворяет условиям совершенной взаимной дополняемости факторов, называется гибким производственным процессом. Производственная функция для системы с гибким производственным процессом, для которой характерна линейная связь между затратами факторов и выпуском продукта, называется линейной производственной функцией.

Линейная производственная функция задаётся уравнением:

y=f(L,K)=aL+bK, (3.27)

где а и b- положительные постоянные.

Следует отметить, что линейная производственная функция не обладает рядом основных свойств, которые присущи по определению неоклассическим производственным функциям. Нарушается первое свойство производственной функции, согласно которому при отсутствии затрат одного из факторов производится нулевой продукт. Пусть затраты труда равны нулю, тогда продукт неокласической производственной функции также равен нулю. Однако, для линейной производственной функции продукт равен:

y=f(0,K)=bK

Другими словами, изокванты линейной производственной функции пересекают оси координат.

Уравнения изокванты линейной производственной функции (ЛПФ) определяются выражением

: (3.28)

Семейство изоквант ЛПФ имеет вид параллельных прямых с угловым

коэффициентом –a/b (рис. 3.16):

Рис. 3.16 Карта изоквант линейной производственной функции.

Экономический смысл ЛПФ: эта функция описывает технологию, характеризующуюся тем, что факторы производства, используемые в производственном процессе, являются абсолютно взаимозаменяемыми, т.е. менеджеру все равно, использовать только труд или только капитал. Понятно, что в реальной жизни такая ситуация вряд ли возможна, потому что машины все равно управляются людьми.

Линейная производственная функция обладает свойством постоянства предельной отдачи каждого фактора производства. Увеличение одного фактора при фиксации затрат другого фактора не уменьшает величину предельной отдачи (производительности) ресурса.

Это позволяет дать экономическую интерпретацию постоянных коэффициентов линейной производственной функции как значений предельной отдачи труда и капитала соответственно:

V_L= a

(3.29)

V_k= b

Для средней отдачи труда и капитала получаем:

(3.30)

где к- фондовооруженность.

Если предельные отдачи ресурсов есть величины постоянные, то средние отдачи изменяются в зависимости от фондовооружённости k. С ростом фондовооруженности средняя производительность труда увеличивается, а средняя отдача капитала уменьшается.

Коэффициенты эластичности выпуска по ресурсам:

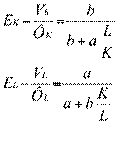(3.31)

Предельная норма замещения труда капиталом для линейной производственной функции есть величина постоянная:

(3.32)

Эластичность замещения труда капиталом линейной производственной функции равна бесконечности, так как .

Определить коэффициенты линейной производственной функции можно методом множественной линейной регрессии по эмпирическим данным о системе производства, которые должны включать величины затрат труда и капитала и количество произведённого продукта.

Несмотря на указанные недостатки линейных производственных функций, они получили широкое распространение при моделировании крупномасштабных производственных систем, таких как отрасли промышленности и национальные экономики, когда выпуск агрегатированного продукта обеспечивается одновременным функционированием огромного множества разнообразных технологических процессов.