Основные свойства и определения производственной функции

Производственные функции определяются двумя группами предположений: математических и экономических.

Математически предполагается, что ПФ должна быть непрерывной и дважды дифференцируемой.

Экономические свойства состоят в следующем:

• при отсутствии хотя бы одного производственного ресурса производство невозможно;

• рост использования ресурсов приводит к росту результата производства;

• увеличение затрат одного ресурса приводит к снижению эффективности его использования.

• При макроэкономическом моделировании используется предположение о пропорциональности роста результата росту затрат ресурсов.

Производственная функция, отвечающая всем перечисленным свойствам, называется неоклассической. В частности, производственная функция Кобба-Дугласа относится к неоклассическим ПФ.

Производственная система является эффективной, если фирма достигает целей при низких издержках, которые пропорциональны количеству потребляемых системой факторов производства за период

времени, при условии постоянства цен на рынке ресурсов. Математически эффективность производственного процесса или эффективность использования факторов производства определяется величиной средней и предельной отдачи ресурса. Более эффективная система производит большее количество продукта при заданных затратах факторов производства в единицу времени. Для понимания производственного процесса являются весьма важными приводимые ниже определения.

Средняя отдача ресурса – это отношение объема выпускаемой фирмой продукции к использованному количеству этого ресурса (затраты остальных факторов остаются неизменными).

i=l,2,...n (3.12)

Если фактором производства является труд, то это – средняя производительность труда.

Если фактором производства является капитал, то это – средняя фондоотдача.

Пример 3.7Производственная система произвела за период времени 150 единиц продукта и затратила 50 единиц капитала и 10 единиц труда. В этом случае, средняя производительность труда Ф_L определяется как Ф_L=150/10=15 единиц продукта на единицу труда, а средняя фондоотдача Ф_k вычисляется по формуле: Ф_k=150/50=3 единицы продукта на единицу капитала.

Предельная отдача ресурса (предельная производительность ресурса) – отношение величины изменения объема производимой продукции к величине изменения ресурса.

Предположим, на фирме работают 6 человек, и они вместе производят в день 90 единиц продукции. Предположим, что владелец фирмы нанял на работу еще одного человека. В результате общий объем продукции стал 98 единиц, т.е. увеличился на 8 единиц, В этом случае 8 единиц это и есть предельная отдача труда.

Если на предприятии работает не 8 человек, а 800 или 1500 человек, тогда прирост объема продукции на 1 единицу трудозатрат будет бесконечно малой величиной, и предельную отдачу переменного фактора можно представить как первую производную производственной функции.

В общем случае:

i=l,2,...n (3.13)

В случае двух факторов K и L :

- предельная фондоотдача (3.14)

предельная производительность труда. (3.15)

Пример 3.8Функционирование производственной системы описывается производственной функцией

f(K,L) = 20K^1/2L^1/2

Пусть за период потрачено 25 единиц капитала и 4 единицы труда.

Рассчитать значения средней и предельной отдачи ресурсов.

Количество произведенного продукта У равно:

У=20*25^1/2*4^1/2 = 200 единиц продукта

Средняя фондоотдача равна:

Фк=200/25=8 единиц продукта на единицу капитала

Средняя производительность труда равна:

Ф_L= 200/4=50 единиц продукта на единицу труда

Предельная фондоотдача равна:

Vk=∂Y/∂K=1/2*20*k-^1/2L^1/2 = 1/2*20*(1/5)*2 = 4 единиц продукта на единицу капитала.

Предельная производительность труда равна:

V_L= ∂Y/∂L = 1/2*20*K^1/2L^-1/2 = 1/2*20*5*(1/2) =25 единиц продукта на единицу труда.

Коэффициенты эластичности выпуска по ресурсам показывают, на сколько процентов изменится объем выпуска продукции при изменении затрат соответствующего производственного ресурса на один процент. В случае двух факторов K и L коэффициенты эластичности определяются следующими формулами:

-коэффициент эластичности продукта по фондам (3.16)

- коэффициент эластичности продукта по труду (3.17)

Коэффициенты эластичности вы­пуска E_k и E_L зависят от того, при каких значениях К и L они подсчитываются.

Эластичность продукта по i-му фактору можно выразить через средние и предельные отдачи фактора производства. Покажем это на примере коэффициента эластичности по фондам:

(3.18)

Таким образом, эластичность продукта по i-му фактору равна отношению величины предельной отдачи фактора к величине средней отдачи этого же фактора.

Пример 3.9Производственная система производит 150 единиц продукта при затратах 50 единиц капитала и 10 единиц труда. Каким станет выпуск продукта, если затраты капитала увеличатся до 54 единиц при постоянных затратах труда. Эластичность продукта по капиталу равна 0,25.

Порядок расчёта производства следующий:

Затраты капитала возросли в абсолютной величине на 4 единицы или в относительной величине на 4*100/50=8%. Это вызовет рост выпуска продукта в относительных величинах на 0,25*8%=2%. В абсолютной величине рост составит 2*150/100=3 единицы продукта. Следовательно, выпуск продукта возрастёт до 153 единиц за период времени.

Пример 3.10Производственная система производит 150 единиц продукта при затратах 50 единиц капитала и 10 единиц труда. Найти количество произведённого продукта при затратах 49 единиц капитала и 11 единиц труда, если коэффициенты эластичности по капиталу и труду равны 0,25 и 0,75 соответственно.

Раскладывая производственную функцию в ряд Тейлора имеем:

f(K + ΔK, L + ΔL) = f + (∂f/∂K)* ΔK + (∂f/∂L)* ΔL = Y + V_k*ΔK + V_L*ΔL

Вычислим приращения затрат капитала и труда:

∆К=49-50=-1; ∆L=11-10=1;

Средние продукты труда и капитала при затратах (50;10) равны:

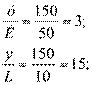
Произведённый продукт у при затратах (49;11) равен:

у(49;11)=150+0,25*3*(-1)+0,75*15*1=160,5 единиц продукта.

Предельная норма замещения ресурсов.Перемещение точки затрат вдоль изокванты сопровождается непрерывным замещением i-го фактора j-м фактором при постоянном уровне производства продукта У. Это приводит к необходимости введения понятия предельной нормы замещения i-го фактора j-м фактором. Предельная норма замещения i-го фактора j-м фактором равна дополнительному количеству j-го фактора, которое компенсирует уменьшение i-го фактора на единицу при постоянном уровне производства продукта и постоянном потреблении других факторов:

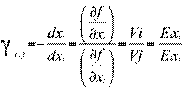(3.19)

Для двухфакторной производственной функции предельная норма замещения капитала трудомпоказывает, сколько единиц ресурса L может быть высвобождено (привлечено) при увеличении (уменьшении) затрат ресурса K на единицу:

(3.20)

Аналогично может быть определена предельная норма замещения труда L капиталом К.

Эластичность замещения ресурсов (σ) используется для количественной оценки скорости изменения предельной нормы замещения.

Величина (σ) показывает, на сколько процентов должно измениться отношение ресурса К к ресурсу L при движении вдоль изокванты, чтобы при этом предельная норма замещения изменилась на один процент (характеризует скорость изменения предельной нормы замещения γ при движении вдоль изокванты).

σ=[∂(K/L)/(K/L)]/(∂γ_LK/γ_LK) (3.21)

Закон уменьшающейся предельной производительности ресурса(или закон убывающей отдачи ресурса – пояснение к третьему свойству производственной функции). Смысл этого закона заключается в следующем. Если некоторые или хотя бы один из факторов производства, которые используются в производственном процессе, являются фиксированными в течение некоторого промежутка времени (например, количество станков предприятия может не изменяться в течение года), тогда предельная производительность переменных факторов производства либо сразу, либо начиная с определенного момента, непременно начнет снижаться.

Например, в краткосрочном периоде переменным фактором производства является труд. Можно изменить количество затрачиваемого труда, нанимая дополнительных работников. Последовательное привлечение дополнительных работников, при фиксированном количестве станков, хотя и будет увеличивать выпуск продукции фирмы, однако этот прирост продукции от работы каждого следующего нанимаемого работника окажется меньше по сравнению с тем приростом продукции, который был получен фирмой от работы предыдущего нанятого ею работника. Это означает, что предельная производительность, т.е. продукт последнего нанятого работника (предельный продукт труда) убывает по мере увеличения числа работников на фирме.

Закон относится не только к убыванию предельной производительности труда. Аналогичным образом он действует применительно к любому другому фактору производства, являющимся переменным. Например, если фиксированы затраты труда, но при этом наращивается количество сырья и материалов, используемых в процессе производства продукта, то материалоотдача от каждой дополнительной единицы затрат сырья будет снижаться.

Влияние масштаба производства и однородность производственной функции. Производственная функция обладает свойством однородности, которое математически выражает отдачу производственной системы от расширения масштабов производства. Пропорциональное увеличение всех факторов производства λ раз не изменяет структуру производства, а приводит к равному для всех факторов изменению средних и предельных продуктов. В общем случае, производственная функция удовлетворяет равенству:

(3.22)

где постояная δ называется степенью однородности производственной функции.

Для случая двух переменных K и L однородность производственной функции f(L,K) определяется в частности:

(3.23)

Неоклассическая производственная функция является однородной функцией первой степени, для которой справедливо:

3.24)

Поэтому говорят, что неоклассическая функция является линейно-однородной.

В случае неклассической производственной функции со степенью однородности равной единице, увеличение масштаба производства (увеличение всех затрат факторов в λ раз) приводит к пропорциональному увеличению выпущенного продукта в λ раз:

(3.25)

Можно доказать, что для производственной функции f(L,K) со степенью однородности равной единице, имеет место тождество, имеющее важное экономическое значение:

(3.26)

Т.е. произведённый продукт Y может быть представлен в виде суммы и разделён на две части. Первое слагаемое V_kК показывает вклад затраченного капитала в полученный продукт Y. Второе слагаемое V_LL представляет вклад затрат труда в произведённом продукте Y. Это позволяет оценить вклад труда и капитала в произведённый продукт.

Пример 3.11.Производственная система описывается производственной функцией со степенью однородности равной единице. Система за период времени произвела 200 единиц продукции, затратив 50 единиц капитала и 10 единиц труда. Коэффициенты эластичности по капиталу и труду равны 0,25 и 0,75. Определить вклад труда и вклад капитала в произведенную продукцию.

Средние отдачи капитала и труда равны:

Предельные отдачи капитала и труда находим с помощью коэффициентов эластичности:

Окончательно, вычисляем вклад затрат капитала и труда в произведённую продукцию:

Следовательно, производственная система создала 50 единиц продукции за счёт потребления 50 единиц капитала и 150 единиц продукции в результате преобразования 10 единиц труда.