
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Балансовые модели в задачах анализа трудовых показателей и показателей использования основных фондов.
Различные модификации рассмотренной выше модели межотраслевого баланса производства и распределения продукции в народном хозяйстве позволяют расширить круг показателей, охватываемых моделью. Рассмотрим применение межотраслевого балансового метода для анализа трудовых показателей.
К числу важнейших аналитических возможностей балансового метода относится определение прямых и полных затрат труда на единицу продукции и разработка на этой основе балансовых продуктово-трудовых моделей, при этом исходной моделью служит отчетный межпродуктовый баланс в натуральном выражении. В этом балансе по строкам представлено распределение каждого отдельного продукта на производство других продуктов и конечное потребление (первый и второй квадранты схемы межотраслевого баланса.) Отдельной строкой дается распределение затрат живого труда в производстве всех видов продукции; предполагается, что трудовые затраты выражены в единицах труда одинаковой степени сложности.
Обозначим затраты живого труда в производстве j – го продукта через Lj, а объем производства этого продукта (валовой выпуск), как и раньше, через Xj. Тогда прямые затраты труда на единицу j – го продукции (коэффициент прямой трудоемкости) можно задать следующей формулой:
 . (4.26)
. (4.26)
Введем понятие полных затрат труда как суммы прямых затрат живого труда и затрат овеществленного труда, перенесенных на продукт через израсходованные средства производства. Если обозначить величину полных затрат труда на единицу продукции j – го вида через Tj, то произведения вида aij Tj отражают затраты овеществленного труда, перенесенного на единицу j – го продукта через i – е средство производства; при этом предполагается, что коэффициенты прямых материальных затрат aij выражены в натуральных единицах. Тогда полные трудовые затраты на единицу j – й продукции (коэффициент полной трудоемкости) будут равны
 . (4.27)
. (4.27)
Введем в рассмотрение вектор-строку коэффициентов прямой трудоемкости t = (t1, t2, …, tn) и вектор-строку коэффициентов полной трудоемкости T = (T1, T2, …, Tn).
Тогда с использованием уже рассматриваемой выше матрицы коэффициентов прямых материальных затрат A (в натуральном выражении) систему уравнений () можно переписать в матричном виде:
T = TA + t. (4.28)
Произведя очевидные матричные преобразования с использованием единичной матрицы Е
Т – ТА = ТЕ – ТА = Т (Е - A) = t, (4.29)
Получим следующее соотношение для вектора коэффициентов полной трудоемкости:
T = t (E - A)-1. (4.30)
Матрица (E - A)-1 представляет матрицу В коэффициентов полных материальных затрат, так что последнее равенство можно переписать в виде
T = t B. (4.31)
Обозначим через L величину совокупных затрат живого труда по всем видам продукции, которая с учетом формулы () будет равна
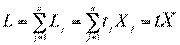 . (4.32)
. (4.32)
Используя соотношения () () и (), приходим к следующему равенству:
tX = TY, (4.33)
где t и T – вектор-строки коэффициентов прямой и полной трудоемкости, а X и Y – вектор-столбцы валовой и конечной продукции соответственно.
Соотношение (4.339) представляет собой основное балансовое равенство в теории межотраслевого баланса труда. В данном случае его конкретное экономическое содержание заключается в том, что стоимость конечной продукции, оцененной по полным затратам труда, равна совокупным затратам живого труда. Сопоставляя потребительский эффект различных взаимозаменяемых продуктов с полными трудовыми затратами на их выпуск, можно судить о сравнительной эффективности их производства. С помощью показателей полной трудоемкости более полно и точно, чем при использовании существующих стоимостных показателей, выявляется структура затрат на выпуск различных видов продукции и прежде всего соотношение между затратами живого и овеществленного труда.
На основе коэффициентов прямой и полной трудоемкости могут быть разработаны межотраслевые и межпродуктовые балансы затрат труда и использования трудовых ресурсов. Схематически эти балансы строятся по общему типу матричных моделей, однако все показатели в них (межотраслевые связи, конечный продукт, условно чистая продукция и др.) выражены в трудовых измерителях.
Рассмотрим пример.
Пример 4.3. Пусть в дополнение к исходным данным примера 4.1 заданы затраты живого труда (трудовые ресурсы) в трех отраслях: L1 = 1160, L2 = 460, L3 = 875 в некоторых единицах измерения трудовых затрат. Требуется определить коэффициенты прямой и полной трудоемкости и составить межотраслевой баланс затрат труда.
1. Воспользовавшись формулой (4.26) и результатами примера 4.1, находим коэффициенты прямой трудоемкости:
 ;
;  ;
;  .
.
2. По формуле (4.31), в которой в качестве матрицы Bберется матрица коэффициентов полных материальных затрат, найденная в примере 4.1, находим коэффициенты полной трудоемкости:
 .
.
3. Умножая первую, вторую и третью строки первого и второго квадрантов межотраслевого материального баланса, построенного в примере 4.1, на соответствующие коэффициенты прямой трудоемкости, получаем схему межотраслевого баланса труда (в трудовых измерителях) (табл.4.5).
Схема межотраслевого баланса труда Таблица 4.5
| Производящие отрасли | Потребляющие отрасли | Затраты труда на конечную продукцию | Затраты труда в отраслях (трудовые ресурсы) | ||
| Межотраслевые затраты овеществленного труда | |||||
| 348,4 350,6 435,7 | 115,8 112,3 89,7 | 60,2 18,3 89,7 | 635,6 458,2 512,6 | 1160,0 939,4 1127,8 |
Незначительные расхождения между данными таблицы и исходными данными вызваны погрешностями округления при вычислениях.
Развитие основной модели межотраслевого баланса достигается также путем включения в нее показателей фондоемкости продукции. В этом случае модель дополняется отдельной строкой, в которой указаны в стоимостном выражении объемы производственных фондов Фj , занятые в каждой j-й отрасли. На основании этих данных и объемов валовой продукции всех отраслей определяются коэффициенты прямой фондоемкости продукции j-й отрасли:
 (4.34)
(4.34)
Коэффициент прямой фондоемкости показывает величину производственных фондов, непосредственно занятых в производстве данной отрасли, в расчете на единицу ее валовой продукции. В отличие от этого показателя коэффициент полной фондоемкости 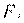 отражает объем фондов, необходимых во всех отраслях для выпуска единицы конечной продукции j-й отрасли. Для коэффициента полной фондоемкости справедливо равенство, аналогичное равенству (4.27) для коэффициента полной трудоемкости:
отражает объем фондов, необходимых во всех отраслях для выпуска единицы конечной продукции j-й отрасли. Для коэффициента полной фондоемкости справедливо равенство, аналогичное равенству (4.27) для коэффициента полной трудоемкости:
 (4.35)
(4.35)
Аналогично преобразованиям, применяемым выше для коэффициентов трудоемкости, можно получить следующее выражение для расчета коэффициентов полной фондоемкости:
 . (4.36)
. (4.36)
Для более глубокого анализа необходимо дифференцировать фонды на основные и оборотные, а в пределах основных на здания, сооружения, производственное оборудование, транспортные средства и т.д.
Дата добавления: 2014-11-13; просмотров: 328; Мы поможем в написании вашей работы!; Нарушение авторских прав |