Виды моделей однопродуктовой одноэтапной задачи размещения и развития производства.

Для получения более точных результатов решения задач РРП следует учесть следующие факторы:

• нелинейная зависимость затрат от объёмов производства продукции. В результате целевая функция должна учитывать эту нелинейность в производственных затратах и линейность в транспортных затратах;

• характер переменной модели. Переменная может быть непрерывной, т.е. объем производства может изменяться от нижнего до верхнего предела, а может быть и дискретной, т.е. принимать определённые значения.

С учётом этих факторов можно выделить два типа моделей задачи РРП:

­ модель нелинейной задачи с непрерывными переменными (безвариантная постановка);

­ модель нелинейной задачи с дискретными переменными (вариантная постановка).

Вид модели безвариантной постановки:

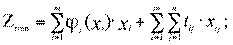(4.53)

(4.54)

где:

ϕ_i(x_i)- функция удельных производственных затрат, показывающая зависимость их уровня от объема производства в пункте i.

d_i- нижний предел мощности производства;

t_ij- транспортные затраты на единицу продукции от i-го пункта производства до j-го потребителя.

Основной путь решения таких задач состоит в минимизации соответствующих нелинейных зависимостей и последующем решении целого ряда линейных задач, а так же выбора из полученных результатов наилучшего варианта, отвечающего требованиям критерия оптимальности. Этот метод носит название аппроксимации кусочно-линейными функциями, в этом случае нелинейную зависимость представляют в виде линейной для более узкого интервала между нижним и верхним пределами интервала.

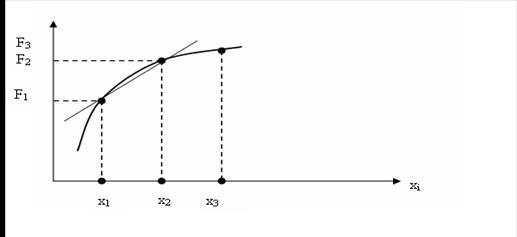
Рисунок 4.2 Представление нелинейной зависимости суммарных затрат от объемов производства.

Выпуклая кривая на графике по определённому интервалу делится на отрезки, крайние точки которых соединяются прямыми. Для каждого из интервалов решаются задачи линейного программирования и находятся значения целевой функции. Из всех вариантов выбирается минимальное значение, ему и будет соответствовать оптимальный план развития производства. Решение тем точнее, чем на большее количество интервалов разделена эта зависимость.

Исходя из специфики химических, металлургических производств мощность предприятия может формироваться за счет крупных неделимых агрегатов и изменяться дискретно. В таких случаях искомые переменные ­ перспективные производственные мощности предприятий могут принимать не любые значения на всем интервале изменения мощности, а лишь некоторые, строго определенные значения, кратные величинам мощностей имеющихся на предприятии агрегатов, технологических линий, т.е. в этом случае получается задача развития и размещения с дискретными (целочисленными) переменными.

Для представления модели задачи РРП с дискретными переменными и нелинейной зависимостью удельных производственных затрат от мощности дополнительно введем следующие обозначения:

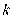­ индекс типового проекта; число используемых типовых проектов для разных пунктов производства неодинаково, поэтому = 1,2,…., ;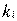

­ мощность предприятия в i-м пункте производства по -му типовому проекту.

В модели (4.53 ÷ 4.54 ) изменится только вид ограничения по возможной мощности в пункте строительства:

(4.55)

Условия (4.55) отражают тот факт, что размер мощности предприятия в i-м пункте может быть равен одному из возможных вариантов типовых проектов (или нулю).