Многопродуктовые задачи развития и размещения производства.

Более широкую сферу применения имеют задачи развития и размещения многономенклатурного производства, т.к. практически любое производство является многопродуктовым. В этих задачах определяются не только пункты нового строительства и расширения (реконструкции) действующих предприятий и размеры производства для них, но и объемы производства каждого продукта в рамках общей мощности предприятия, т.е. специализация.

Задача ставится следующим образом: определить пункты строительства, мощности и специализацию многономенклатурных производств при известной потребности каждого из потребителей в каждом виде продукции и известной зависимости затрат от объёма производства данной продукции, а так же транспортных затрат на перевозку единицы каждого вида продукции по каждому направлению.

Введем обозначения:

_i - пункта производства (строительства), ;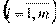

_j - индекс пункта потребления,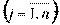

_k - индекс видов продукции, ;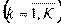

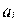─ максимально возможная мощность предприятия в пункте i;

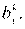─ размер потребности пункта j в продукции вида к;

─ затраты на производство единицы продукции вида k в пункте i в части, зависящей от специализации (и функционально зависящие объема выпуска k -го вида продукции);

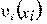─ удельные затраты на производство единицы продукции в пункте i в части, функционально зависящие от концентрации, т.е. от общей мощности предприятия в данном пункте);

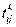─ транспортные затраты на перевозку единицы k -ой продукции от i-пункта к j-му потребителю;

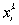─ объем производства k-ой продукции на i-ом предприятии;

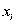─ общая мощность предприятия в i-ом пункте строительства;

─ объем поставок k-ой продукции от i-пункта к j-му потребителю.

Модель нелинейной безвариантной задачи размещения многономенклатурного производства при принятых обозначениях выглядит следующим образом.

Совокупные затраты на производство и перевозку всех видов продукции от всех пунктов строительства ко всем потребителям должны быть минимальными

(4.67)

при выполнении следующих ограничений:

• потребность каждого потребителя должна быть удовлетворена по каждому виду продукции

; (4.68)

• объем вывоза каждого вида продукции от каждого предприятия должен быть равен объему производства

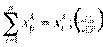; (4.69)

• суммарный выпуск всех видов продукции предприятия не должен превосходить максимально возможных размеров производства в данном пункте

; (4.70)

• неотрицательность переменных

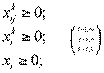. (4.71)

Раздельный учет в целевой функции (4.67) производственных затрат 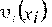и вызван различным характером зависимости отдельных статей или категорий затрат от концентрации и специализации производства. Так, например, общезаводские расходы (в составе текущих затрат) и капитальные вложения в пассивную часть фондов (в составе единовременных затрат) зависят лишь от общей мощности предприятия (т.е. концентрации) и, как правило, мало зависят от структуры выпуска продукции по видам. И наоборот, затраты на сырье и на приобретение основного технологического оборудования служат примером той части текущих и единовременных затрат, которые непосредственно зависят от размеров выпуска того или иного вида продукции (т.е. от специализации).

В этом разделе рассмотрена безвариантная модель развития производства, т.к. мощность и специализация каждого предприятия не выбираются из заранее заданных вариантов (проектов), а формируются в процессе решения задачи.

Существуют другие модификации задач, учитывающих некоторые отраслевые особенности, например вариантная или сетевая модели. Одну из них, вариантную, рассмотрим в следующем разделе.