Модель Эберса-Молла

Модель Эберса-Молла построена для биполярного транзистора, работа которого описана в разд. 3.2. Прохождение токов БТ в этой модели представлено взаимодействием работы двух р-n-переходов, что отражает нормальное и инверсное включение (рис.3.7).

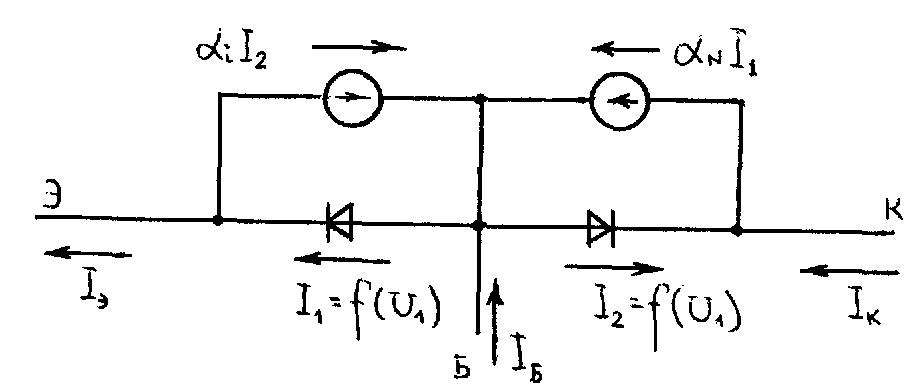
Рисунок 3.7– Эквивалентная схема, соответствующая модели Эберса-Молла n-р-n-транзистора

Токи эмиттера и коллектора из рис. 3.7

(3.19)

где , – напряжение на эмиттерном и коллекторном переходах, соответственно; , – обратные токи насыщения эмиттерного и коллекторного переходов (обратные токи идеализированной модели БТ) в режиме короткого замыкания (К.З.) электродов база-коллектор и база-эмиттер, соответственно.

Как правило, обратные токи переходов в БТ определяют в режиме холостого хода (Х.Х.), т.е. при «обрыве» третьего электрода. Для определения соотношения между обратными токами переходов, измеренных в режимахХ.Х. и К.3., запишем выражения (3.19)при условиях, что I_э = 0 и коллекторный переход смещен в обратном направлении:

(3.20)

где 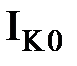– обратный ток коллекторного перехода идеализированной модели БТ, измеренной в режиме Х.Х.

.

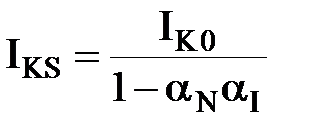(3.21)

Если воспользоваться выражением (3.19) при условиях, что и что эмиттерный переход смещен в обратном направлении, то по аналогии с (3.21) получим

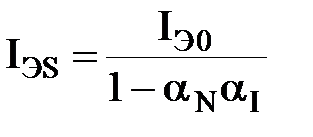
(3.22)

Так как обычно произведение 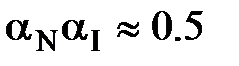, то для практических расчетов следует запомнить, что . Следует также запомнить соотношение между обратными токами коллекторного и эмиттерного переходов

(3.23)

Воспользовавшись (3.19), (3.21) и (3.22), запишем выражения для токов электродов одномерной идеализированной модели БТ:

;	(3.24)
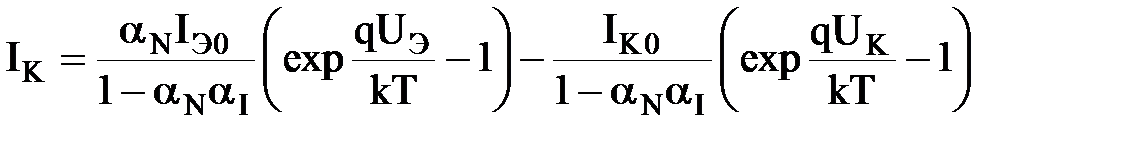;	(3.25)
	(3.26)