Теорема о моменте равнодействующей силы (теорема Вариньона).

Теорема: момент равнодействующей системы сил относительно любой точки равен геометрической сумме моментов всех сил этой системы относительно той же точки. Момент равнодействующей силы относительно произвольной оси равен алгебраической сумме моментов сил системы относительно той же оси.

На твердое тело действует произвольная система сил , имеющая равнодействующую силу , т.е. .

К заданной системе сил добавим ее уравновешивающую силу .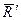

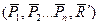
0.

Получим в результате систему эквивалентную нулю, следовательно, можно записать условия равновесия, в частности, геометрическая сумма моментов сил этой новой системы относительно любой точки О равен нулю.

,

но ,

получим

Если правую и левую часть этого выражения спроектировать на произвольную ось OZ, получим