Перенесение заданного горизонтального расстояния

Пусть требуется перенести на местность точку Р с заданными в проекте координатами х_Р, у_Р. Для решения этой задачи необходимо иметь не менее двух опорных точек А и В с известными координатами х_А, у_А, х_B, у_B и дирекционным углом (АВ).

В зависимости от условий местности и взаимного расположения точек Р, А и В применяют различные способы переноса точки Р в натуру.

Полярный способ (рис. 13.2, а) применяют в открытой местности при благоприятных условиях для линейных измерений. При этом перенос точки Р осуществляют по двум разбивочным элементам — горизонтальному углу β и горизонтальному расстоянию l.

Если значения величин β и l не даны в проекте, то их определяют решением обратной геодезической за дачи.

(13.2)

Положение точки Р на местности определяют отложением в точке А горизонтального угла β и по полученному направлению расстояния l способами, описанными выше.

Рис. 13.2. Перенесение в натуру точки Р по заданным ее координатам х и у

Способ угловой засечки (рис. 13.2, б) применяют при неблагоприятных условиях для линейных измерений и при больших расстояниях до точки Р. При этом перенос точки Р в натуру осуществляют только по угловым величинам β_А и β_В. Для определения величин углов сначала, решив обратную геодезическую задачу, вычисляют значения дирекционных углов (АР) и (ВР), а затем находят требуемые углы из выражений

где (АВ) — дирекционный угол известного направления АВ.

В точках А и В устанавливают теодолиты и, отложив углы β_А и β_В, вблизи места пересечения полученных направлений отмечают точки 1, 2, 3, 4. Положение выносимой в натуру точки Р определяют в точке пересечения двух шнуров, натянутых по линиям 1—2 и 3—4.

Способ линейных засечек (рис. 13.2, в) применяют при расстояниях l_А и l_В определяемой точки Р от опорных пунктов А и В не более длины мерного прибора (рулетки).

Если горизонтальные расстояния l_А и l_В не даны в проекте, то их значения получают по формулам

(13.3)

При наклонной местности по формуле (13.1) вычисляют соответствующие им наклонные расстояния L_А и L_В . От точек А и В с помощью двух рулеток откладывают эти расстояния и в точке совмещения их концов закрепляют точку Р.

Способ створов применяют тогда, когда подлежащая разбивке точка Р расположена в створе линии между известными точками А и В или на ее продолжении. При этом задача сводится к откладыванию вдоль линии створа проектного расстояния от ближайшей точки А или В до точки Р в заданном направлении.

Способ ординат (перепендикуляров) заключается в откладывании под прямым углом к линии АВ заданного расстояния. При этом вначале определяют точку Е, а затем, установив на ней теодолит, отложив угол β, равный 90°, и расстояние S₂, находят точку С.

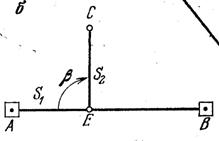Рис. 13.3. Способ перпендикуляров.