Общая постановка задачи линейного программирования. Экономико-математическая модель

Экономико-математическая модель

В настоящее время в литературе насчитывается несколько десятков определений понятия "модель", отличающихся друг от друга.

Тем не менее, это понятие знакомо каждому: например, игрушечный самолет, бумажный голубь – модели самолета. Менее привычно представление о том, что фотоснимок пейзажа, географическая карта – это модель местности. И, наверное, новым для многих является то, что знакомая со школьных лет формула пути s = vt – математическая модель. Под моделью будем понимать условный образ какого-либо объекта, приближенно воссоздающий этот объект с помощью некоторого языка. В экономико-математических моделях таким объектом является экономический процесс (например, использование ресурсов, распределение изделий между различными типами оборудования и т.п.), а языком – классические и специально разработанные математические методы.

Экономико-математическая модель – математическое описание исследуемого экономического процесса или объекта. Эта модель выражает закономерности экономического процесса в абстрактном виде с помощью математических соотношений. Использование математического моделирования в экономике позволяет углубить количественный экономический анализ, расширить область экономической информации, интенсифицировать экономические расчеты.

Можно выделить три основных этапа проведения экономико-математического моделирования. На первом этапе ставятся цели и задачи исследования, проводится качественное описание объекта в виде экономической модели. На втором этапе формируется математическая модель изучаемого объекта, осуществляется выбор (или разработка) методов исследования, проводится программирование модели на ЭВМ, подготавливается исходная информация. Далее проверяются пригодность машинной модели на основании правильности получаемых с ее помощью результатов и оценка их устойчивости.

На третьем, основном, этапе экономико-математического моделирования осуществляются анализ математической модели, реализованной в виде программ для ЭВМ, проведение машинных расчетов, обработка и анализ полученных результатов.

Примеры задач линейного программирования

Задача об использовании ресурсов (задача планирования производства)

1.1. Для изготовления двух видов продукции и используют четыре вида ресурсов и . Запасы ресурсов, число единиц ресурсов, затрачиваемых на изготовление единицы продукции, приведены в табл. 1.1 (цифры условные).

Таблица 1.1

Вид ресурса	Запас ресурса	Число единиц ресурсов, затрачиваемых на изготовление единицы продукции
		–
			–

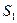
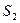
Прибыль, получаемая от единицы продукции и – соответственно 2 и 3 руб.

Необходимо составить такой план производства продукции, при котором прибыль от ее реализации будет максимальной.

Решение. Составим экономико-математическую модель задачи.

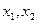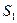Обозначим – число единиц продукции соответственно и , запланированных к производству. Для их изготовления (см. табл. 1.1) потребуется единиц ресурса , единиц ресурса , единиц ресурса и 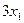единиц ресурса . Так как потребление ресурсов и не должно превышать их запасов, соответственно 18, 16, 5 и 21 единицы, то связь между потреблением ресурсов и их запасами выразится системой неравенств:

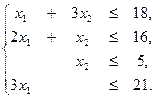(1.1)

По смыслу задачи переменные

(1.2)

Суммарная прибыль F составит руб. от реализации продукции и руб. – от реализации продукции , т.е.

(1.3)

Итак, экономико-математическая модель задачи: найти такой план выпуска продукции 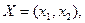, удовлетворяющий системе (1.1) и условию (1.2), при котором функция (1.3) принимает максимальное значение.

Задачу легко обобщить на случай выпуска n видов продукции с использованием m видов ресурсов.

Обозначим – число единиц продукции 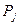, запланированной к производству; 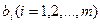– запас ресурса – число единиц ресурса 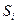, затрачиваемого на изготовление единицы продукции 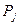(числа часто называют технологическими коэффициентами); 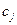– прибыль от реализации единицы продукции .

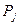Тогда экономико-математическая модель задачи об использовании ресурсов в общей постановке примет вид: найти такой план выпуска продукции, удовлетворяющий системе

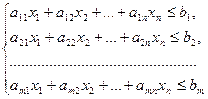(1.4)

и условию

(1.5)

при котором функция

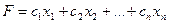(1.6)

принимает максимальное значение.