Линейного программирования

Множество допустимых решений (многогранник решений) задачи линейного программирования представляет собой выпуклый многогранник (или выпуклую многогранную область), а оптимальное решение задачи находится, по крайней мере, в одной из угловых точек многогранника решений.

Рассмотрим задачу в стандартной форме (1.4)–(1.6) с двумя переменными (n=2). К такой форме может быть сведена и каноническая задача (с ограничениями в виде уравнений), когда число переменных я больше числа уравнений m на 2, т.е. n-m=2.

Пусть геометрическим изображением системы ограничений является многоугольник ABCDE (рис. 2.1). Необходимо среди точек этого многоугольника найти такую точку, в которой линейная функция принимает максимальное (или минимальное) значение.

Рассмотрим так называемую линию уровня линейной функции F, т.е. линию, вдоль которой эта функция принимает одно и то же фиксированное значение а, т.е. F=а, или

(2.1)

Линии уровня широко используются, например, на картах прогноза погоды, где извилистые линии – так называемые изотермы есть не что иное, как линии уровня температуры Т=с.

Еще более простым примером линий уровня являются параллели на географической карте. Это линии уровня широты.

На многоугольнике решений следует найти точку, через которую проходит линия уровня функции F с наибольшим (если линейная функция максимизируется) или наименьшим (если она минимизируется) уровнем.

Уравнение линии уровня функции (2.1) есть уравнение прямой линии. При различных уровнях а линии уровня параллельны, так как их угловые коэффициенты определяются только соотношением между коэффициентам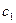и и и, следовательно, равны. Таким образом, линии уровня функции F — это своеобразные "параллели", расположенные обычно под углом к осям координат.

Важное свойство линии уровня линейной функции состоит в том, что при параллельном смещении линии в одну сторону уровень только возрастает, а при смещении в другую сторону – только убывает.

Пусть имеются три линии уровня

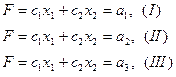
причем линия II заключена между линиями I и III. Тогда или

В самом деле, на штриховой линии (перпендикулярной к линиям уровня на рис. 2.2) уровень является линейной функцией, а значит, при смещении в одном из направлений возрастает, а в другом — убывает.

Для определения направления возрастания рекомендуется изобразить две линии уровня и определить, на которой из них уровень больше. Например, одну из линий можно взять проходящей через начало координат (если линейная функция имеет вид , т.е. без свободного члена, то это соответствует нулевому уровню). Другую линию можно провести произвольно, так, например, чтобы она проходила через множество решений системы ограничений. Далее, определив направление возрастания линейной функции (обозначим его вектором ), найдем точку, в которой функция принимает максимальное или минимальное значение, подобно тому как на карте находится самая северная или самая южная точка (на рис. 2.1 – это точка С или А).

2.1. Решить геометрически 1-ю задачу из разд. 1.2:

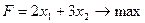
при ограничениях:

Решение. Изобразим многоугольник решений на рис. 2.3. Очевидно, что при F=0 линия уровня проходит через начало координат (строить ее не обязательно). Зададим, например, F=6 и построим линию уровня . Ее расположение указывает на направление возрастания линейной функции (вектор ). Так как рассматриваемая задача – на отыскание максимума, то оптимальное решение – в угловой точке С, находящейся на пересечении прямых I и II, т.е. координаты точки С определяются решением системы уравнений откуда , , т.е. С(6;4).

Максимум (максимальное значение) линейной функции равен

Итак, при оптимальном решении , , т.е. максимальная прибыль в 24 руб. может быть достигнута при производстве 6 единиц продукции и 4 единиц продукции

Рассмотренный в этой главе геометрический метод решения задач линейного программирования обладает рядом достоинств. Он прост, нагляден, позволяет быстро и легко получить ответ.

Однако только геометрический метод решения никак не может удовлетворить ни математиков, ни экономистов. Возможны "технические" погрешности, которые неизбежно возникают при приближенном построении графиков. Второй недостаток геометрического метода заключается в том, что многие величины, имеющие четкий экономический смысл (такие, как остатки ресурсов производства, избыток питательных веществ и т.п.), не выявляются при геометрическом решении задач. Но самое главное – геометрический метод неприемлем для решения практических задач. Его можно применить только в том случае, когда число переменных в стандартной задаче равно двум. Поэтому необходимы аналитические методы, позволяющие решать задачи линейного программирования с любым числом переменных и выявить экономический смысл входящих в них величин.