Кручення прямого бруса круглого перерізу. Основні гіпотези. Напруження в поперечному перерізі брусу. Кут закручення. Полярні моменти інерції для круга та кільця. Момент опору.

Кручення – це один з простих видів навантаження (деформування) бруса, при якому у поперечному перерізі бруса діє тільки внутрішній крутний момент ( ). Брус, навантажений крутним моментом, називають валом (незалежно від форми перерізу).

Розглянемо задачу кручення круглого вала (рис. 8) з геометричної, статичної та фізичної сторін.

Теоретичні і експериментальні дослідження деформації кручення круглого вала дають підстави прийняти таку геометричну модель (рис. 8 а):

1 Вісь вала при крученні залишається прямолінійною.

2 Поперечні перерізи вала, плоскі до деформації, залишаються в своїй площині і лише повертаються навколо осі вала. Таким чином, відстані між поперечними перерізами вала у процесі деформації не змінюються.

3 Радіуси перерізу залишаються при крученні прямолінійними.

Рис. 8 – Модель кручення круглого вала

Кручення у відповідності з цією моделлю подається як результат зсувів, визначених взаємним обертанням перерізів. Кут закручення вважаємо лінійною функцією , тобто погонний (відносний) кут закручення не змінюється по довжині вала:

. (3)

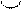Прямолінійна твірна 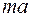(рис. 8 а), нанесена на поверхні вала, перетворюється у гвинтову лінію . Для неї відносний зсув (кут зсуву)

. (4)

Якщо уявно вирізати циліндр радіуса , то твірна на його поверхні перетворюється у гвинтову лінію . При закрученні на той же кут 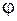дуга 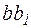менша, ніж дуга , тому і відносний зсув буде меншим:

. (5)

Рівняння (5) встановлює закон зростання кутових деформацій 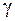пропорційно відстані від осі вала. Це ключове рівняння для геометричної сторони задачі кручення.

Розглянемо статичну сторону задачі. Зробимо переріз на довільній відстані від затиснення (рис. 8 а). При зсуві в поперечних перерізах вала виникають тільки дотичні напруження. Виділимо на перерізі (рис. 5, б) нескінченно малу площадку 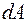на відстані від осі вала. Дотична сила , яка діє на цій площадці, створює відносно осі вала елементарний момент . Повний момент внутрішніх сил (внутрішній крутний момент)

. (6)

У цьому рівнянні шуканою величиною є закон розподілу дотичних напружень 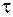, а момент вважаємо вже визначеним за зовнішніми навантаженнями з умов рівноваги відрізаної частини вала.

Фізична сторона задачі представлена законом Гука при зсуві

. (7)

З розв’язувальної системи рівнянь (5) – (7) після підстановки (5) у (7), а потім у (6) маємо:

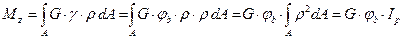, (8)

звідкіля отримає розрахункову формулу для погонного кута закручення:

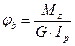, (9)

де добуток називається жорсткістю при крученні.

Повний кут закручення

(10)

Якщо вал має декілька ділянок, що відрізняються розмірами перерізів і значенням крутного моменту, то повний кут закручення дорівнює алгебраїчній сумі кутів закручення окремих ділянок.

Після підстановки (9) у (5), а потім у (7) отримаємо загальну формулу дотичних напружень у довільній точці перерізу закручуваного вала:

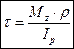(11)

Таким чином, дотичні напруження при крученні зростають за лінійним законом пропорційно відстані точки перерізу від осі вала, згідно з епюрою 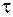(рис.8 б). В точках, однаково віддалених від осі, напруження 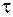рівні за величиною, а спрямовані перпендикулярно радіусу-вектору даної точки.

Максимальні напруження діють у найвіддаленіших від осі точках перерізу, при :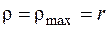

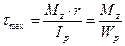, (12)

де – полярний момент опору.

Умова міцності при крученні

, (13)

де – допустиме напруження при крученні; .

При необхідності перевіряють також умову жорсткості вала

, (14)

де – допустимий погонний кут закручення.

В цих формулах внутрішній крутний момент у довільному перерізі дорівнює алгебраїчній сумі зовнішніх крутних моментів, розташованих з однієї сторони від перерізу.

Питання для самоконтролю

1. Запишіть умову міцності при крученні. Які три типи задач вона дозволяє розв'язувати?

2. Що таке жорсткість перерізу при крученні?

3. Напишіть формулу для визначення відносного і повного кута закручування.

4. Поясніть, чому вал кільцевого перерізу при крученні економічні­ший за вал суцільного перерізу.

5. Порядок розрахунку вала на міцність і жорсткість.

6. Як обчислити величину осідання циліндричної гвинтової пружини при стиску?

7. Як зміняться дотичні напруги в пружині /за інших однакових величин/, якщо діаметр дроту збільшити /зменшити/ удачі?