Атомное ядро. Радиоактивность

Закон Мозли позволяет определить количество протонов в ядреи его заряд

Q = Zе:

.

где R - постоянная Ридберга;

- частота К - линии характеристического рентгеновского излучения;

Z - зарядовое число.

Формула Резерфорда позволяет определить заряд ядра Zе и его массовое число А. Экспериментально определяется относительное число a - частиц dN/N, рассеянных в пределах телесного угла dW ядрами атомов исследуемого вещества:

или ,

где n – концентрация атомов;

d – толщина фольги;

k = 9×10⁹ Н×м²/Кл² – коэффициент системы СИ;

T – кинетическая энергия a - частицы;

Z₁e – заряд a - частицы;

- концентрация ядер, выраженная через массовое число A;

r - плотность вещества;

M_ат » m_N – масса атома.

Рассеяние рассчитывается в пределах углов q, q + dq.

Формула, связывающая прицельное расстояние b с углом q рассеяния a-частиц, позволяющая оценить размеры ядра:

.

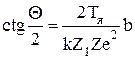Примечание: Прицельное расстояние b принимается за размеры ядра, если q= 90°.

Эффективное сечение ядра s является характеристикой ослабления параллельного пучка частиц в результате их взаимодействия с ядрами вещества. Ядро можно представить непроницаемой площадкой площадью s, перпендикулярной к падающему пучку, которая выводит из потока частицы, пересекающие эту площадку.

Значение s вычисляют по формуле

где n×d - количество ядер фольги, приходящихся на единицу площади;

dN - число рассеянных частиц;

N - число падающих.

Если необходимо определить эффективное сечение ядра, рассеивающего частицы в пределах углов от q до q + dq, то из формулы можно найти площадь круга ds, описанного вокруг ядра с радиусом b (рис.1.1), проходя через который частица рассеивается в пределах заданных углов

ds=2pbdb.

В первом приближении можно считать, что ядро имеет форму шара, радиус которого равен r=r₀×A^1/3 (r₀=1,4×10^-15 м).

Массовое число ядра (число нуклонов в ядре)

A = Z + N,

где Z - зарядовое число (число протонов в ядре);

N - число нейтронов в ядре.

Закон радиоактивного распада

dN = -l×N×dt, или ,

где dN - число ядер, распадающихся за интервал времени dt;

N₀ - число ядер в момент времени, принятый за начальный;

N - число ядер, не распавшихся к моменту времени t;

l - постоянная радиоактивного распада.

Число ядер, распавшихся за время t

.

В случае, если интервал времени Dt, за который определяется число распавшихся ядер, много меньше периода полураспада T_1/2, то число распавшихся ядер можно определять по формуле

DN = l×N×Dt.

Зависимость периода полураспада от постоянной радиоактивного распада

T_1/2 = (ln2)/l = 0,693/l.

Среднее время t жизни радиоактивного ядра, т.е. интервал времени, за который число нераспавшихся ядер уменьшается в e раз

t = 1/l.

Если при радиоактивном распаде ядер N₁ возникают новые радиоактивные ядра N₂, то скорость изменения N₁ с течением времени описывается уравнением

,

а N₂ уравнением

.

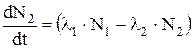Решение последней системы для случая, когда N₀₂ = 0 имеет вид

Вековое уравнение - выражает условие радиоактивного равновесия при условии, когда материнские ядра являются долгоживущими и выполняется условие T₁>>T₂ (l₁<<l₂). Для достаточно большого t ( >>1) его можно записать в виде

N₂(t)l₂ = N₁(t)l₁

Число N атомов, содержащихся в радиоактивном изотопе

,

где m - масса изотопа;

m - молярная масса;

N_A - постоянная Авогадро.

Активность A радиоактивного изотопа

A = - dN/dt = lN или ,

где dN- число ядер, распадающихся за интервал времени dt;

A_o - активность изотопа в начальный момент времени.

Удельная активность изотопа

a = A/m.

Масса ядра - состоит из масс нуклонов, входящих в его состав. Вследствие действия ядерных сил масса ядра оказывается меньше суммы масс его нуклонов

Dm = Z×m_p+(A-Z)m_n - M_я;

Dm = Z×m_H+(A-Z)m_n – M_ат(Z-A);

Dm = Z×D_H+(A-Z)D_n – D_ат;

Dm = =Z×m_H+(A-Z)m_n – M_ат(Z-A) – (M_ат=A+D_ат),

где - m_p масса протона;

m_n - масса нейтрона;

М_я - масса ядра;

Dm - дефект массы ядра;

М_н - масса атома водорода;

М_ат - масса атома;

Dm – дефект массы;

A - массовое число;

D_H, D_n, D_ат - избыток масс атома водорода, нейтрона и атома, который рассматривается.

Энергия связи и дефект массы связаны соотношением

Е_св = Dmс².

Удельная энергия связи

de=Е_св/А.

Примечание. В ядерной физике используется система единиц, в которой скорость света с=1. В такой системе единиц Е = m. В предыдущих формулах масса выражается в атомных; единицах массы (а.е.м). Чтобы перейти от единиц массы к единицам энергии, используется соотношение

1 а.е.м. = 931,44 МэВ.

Формула Вейцзекера (полуэмперическая) позволяет теоретически найти массу ядра и энергию связи (если заданы А и Z). Ядро рассматривается с точки зрения капельной модели:

M_я = Z×m_p + (A-Z)m_n – 14A + 13A^2/3 0,584×Z²/A^1/3 +19,3× .

Энергия связи по формуле Вейцзекера выражается полуэмперической формулой:

E_св=14A-13A^2/3-0,584Z²/A^1/3-19,3 .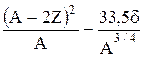

Примечания. 1. Энергия связи выражается в МэВ.

2. d может принимать следующие значения:

Спин ядра, полный механический момент атома, магнитный момент ядра, сверхтонкое расщепление

Механический момент ядра I

,

где i - квантовое число.

Примечание. Свойства момента таковы, что опытным путем можно определить лишь его проекцию I_z на избранное направление (направление можно задать внешним магнитным полем):

I_z=m_i×ħ,

где квантовое число m_i принимает значения m_i = i, i-1, i-2, ... , -i.

Спин ядра - максимальное значение проекции механического момента ядра . Эта характеристика ядра приводится в таблицах.

Полный момент атома представляет собой векторную сумму полных моментов ядра и электронной оболочки :

. (***)

При постоянных значениях и их ориентация может быть разной, поэтому разным будет и значение вектора (рис.1.3). Величина , где F - квантовое число.

Рис.1.2

Возможные значения квантового числа F определяются правилами сложения квантовых векторов и :

ê ê = I +.J; I +.J-1; I + J-2; êI-Jê.

Если I < J, то число значений F будет 2I+1, а если I < J, то их будет 2J+1.

Магнитный момент ядра связан со спиновым моментом следующим соотношением

m_Я = g×I,

где g-скаляр, который называется ядерным гиромагнитным отношением.

Дополнительная энергия атома – возникает в результате взаимодействия ядерного магнитного момента с магнитным полем электронной оболочки ( )

W= .

Значение дополнительной энергии атома (с учетом квантовых чисел F, J, I и известных соотношений , )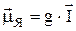

,

где а и g - постоянные.

Значение дополнительной энергии атома (с учетом скалярного произведения )

W = g×a(F² – I² –J²)/2.

Примечание. При заданных I и J, энергия взаимодействия атома W принимает столько значений, сколько их имеет полное квантовое число F: (2I+1 или 2J+ 1). Эта энергия взаимодействия приводит к появлению сверхтонкой структуры энергетических уровней, проявляющихся в сверхтонкой структуре спектральных линий.

Правила отбора для F

DF = 0; ±1.

2.4. Теплоёмкость кристаллов

Средняя энергия квантового одномерного осциллятора

<e> = e_o + ħw/(exp(ħw/(kT)) - 1),

где e_o - нулевая энергия (e_o = ħw/2);

ћ - постоянная Планка, делённая на 2p;

w -циклическая частота колебаний осциллятора;

k - постоянная Больцмана;

T - термодинамическая температура.

Молярная внутренняя энергия системы, состоящей из невзаимо-действующих квантовых осцилляторов

U_m = U_om + 3R×q_E/(exp(q_E/T) - 1),

где R - универсальная газовая постоянная;

q_E = ћw/k - характеристическая температура Эйнштейна;

U_om = 3Rq_E/2 - молярная нулевая энергия Эйнштейна.

Молярная теплоёмкость кристаллического твёрдого тела в области низких температур (T < q_D - предельный закон Дебая)

.

Теплота, необходимая для нагревания тела

,

где m - масса тела;

m - молярная масса;

T₁ и T₂ - начальная и конечная температуры тела.