КОНТРОЛЬНАЯ РАБОТА 6

Таблица вариантов

201. На сколько изменилась кинетическая энергия электрона в атоме водорода, если при переходе в невозбуждённое состояние атом излучил фотон с длиной волны l = 486 нм?

202. D-линия натрия излучается в результате такого перехода электрона с одной орбиты атома на другую, при котором энергия атома уменьшается на DW = 3,37×10^-19 Дж. Найти длину волны l D-линии.

203. Электрон, пройдя разность потенциалов U = 4,9 В, сталкивается с атомом ртути и переводит его в первое возбуждённое состояние. Какую длину волны l имеет фотон, соответствующий переходу атома ртути в основное состояние?

204. Вычислить энергию e фотона, испускаемого при переходе электрона в атоме водорода с третьего энергетического уровня на первый.

205. Определить наименьшую e_min и наибольшую e_max энергии фотона в ультрафиолетовой серии спектра водорода (серии Лаймана).

206. Определить потенциальную П, кинетическую Т и полную Е энергии электрона, находящегося на первой орбите атома водорода.

207. Определить длину волны l, соответствующую третьей спектральной линии в серии Бальмера.

208. Найти наибольшую l_max и наименьшую l_min длины волн в первой инфракрасной серии спектра водорода (серии Пашена).

209. Вычислить длину волны l , которую испускает ион гелия Не⁺ при переходе со второго энергетического уровня на первый. Сделать такой же подсчет для иона лития Li⁺⁺.

210. Найти энергию ионизации E_i и потенциал ионизации U_i ионов Не⁺ и Li⁺⁺.

211. Вычислить частоты n₁ и n₂ вращения электрона в атоме водорода на второй и третьей орбитах. Сравнить эти частоты с частотой n излучения при переходе электрона с третьей на вторую орбиту.

212. Атом водорода в основном состоянии поглотил квант света с длиной волны l =121,5 нм. Определить радиус r электронной орбиты возбужден-ного атома водорода.

213. Определить первый потенциал U₁ возбуждения атома водорода.

214. Атомарный водород, возбужденный светом определенной длины волны, при переходе в основное состояние испускает только три спектральные линии. Определить длины волн этих линий и указать, каким сериям они принадлежат.

215. Фотон с энергией e =16,5 эВ выбил электрон из невозбужденного атома водорода. Какую скорость V будет иметь электрон вдали от ядра атома?

216. На дифракционную решётку нормально падает пучок света от разрядной трубки, наполненной атомарным водородом. Постоянная решётки d=5 мкм. Какому переходу электрона соответствует спектральная линия, наблюдаемая при помощи этой решётки в спектре пятого порядка под углом j=41^o?

217. Какую наименьшую энергию W_min должны иметь электроны, чтобы при возбуждении атомов водорода ударами этих электронов появились все линии всех серий спектра водорода? Какую наименьшую скорость v_min должны иметь эти электроны?

218. Определить изменение энергии DE электрона в атоме водорода при излучении атомом фотона с частотой n = 6,28×10¹⁴ Гц.

219. Во сколько раз изменится период Т вращения электрона в атоме водорода, если при переходе в невозбуждённое состояние атом излучил фотон с длиной волны l= 97,5 нм?

220. В однозарядном ионе лития электрон перешёл с четвёртого энергетического уровня на второй. Определить длину волны l излучения, испущенного ионом лития.

221. В каких пределах должна лежать энергия бомбардирующих электронов, чтобы при возбуждении атомов водорода ударами этих электронов спектр водорода имел только одну спектральную линию?

222. В каких пределах должны лежать длины волн l монохроматического света, чтобы при возбуждении атомов водорода квантами этого света радиус орбиты электрона увеличился в 9 раз.

223. Вычислить радиусы r₂ и r₃ второй и третьей орбит в атоме водорода.

224. Определить скорость V электрона на второй орбите атома водорода.

225. Определить частоту обращения электрона на второй орбите атома водорода.

226. Какую энергию необходимо дополнительно сообщить электрону, чтобы его дебройлевская длина волны уменьшилась от 100 до 50 пм?

227. Две одинаковые нерелятивистские частицы движутся перпендикулярно друг к другу с дебройлевскими длинами волн l₁ и l₂. Найти дебройлевскую длину волны каждой частицы в системе центра инерции.

228. Найти дебройлевскую длину волны релятивистских электронов, подлетающих к антикатоду рентгеновской трубки, если длина волны коротковолновой границы сплошного рентгеновского спектра l_k равна 10,0 пм.

229. При каком значении кинетической энергии дебройлевская длина волны электрона равна его комптоновской длине волны?

230. Из катодной трубки на диафрагму с узкой прямоугольной щелью нормально к плоскости диафрагмы направлен поток моноэнергетических электронов. Определить анодное напряжение трубки, если известно, что на экране, отстоящем от щели на расстоянии L = 0,5 м, ширина центрального дифракционногомаксимума Dx = 10,0 мкм. Ширину b щели принять равной 0,10 мм.

231. Параллельный поток электронов, ускоренных разностью потенциалов U = 25 В, падает нормально на диафрагму с двумя узкими щелями, расстояние между которыми d = 50 мкм. Определить расстояние между соседними максимумами дифракционной картины на экране, расположенном на расстоянии L = 100 см от щелей.

232. Найти дебройлевскую длину волны молекул водорода, соответствующую их наиболее вероятной скорости при комнатной температуре.

233. Найти длину волны де Бройля для электрона, движущегося по первой боровской орбите атома водорода.

234. Заряженная частица, ускоренная разностью потенциалов U = 200 В, имеет длину волны де Бройля l_Б = 2,02 пм. Найти массу частицы, если её заряд численно равен заряду электрона.

235. Альфа-частица движется по окружности радиусом r = 8,3 мм в однородном магнитном поле, напряжённость которого H = 18,9 кА/м. Найти для неё длину волны де Бройля.

236. На сколько по отношению к комнатной должна измениться температура идеального газа, чтобы дебройлевская длина волны его молекул уменьшилась на 20%?

237. Вычислить наиболее вероятную дебройлевскую длину волны молекул водорода, находящихся в термодинамическом равновесии при комнатной температуре.

238. Кинетическая энергия электрона равна удвоенному значению его энергии покоя (2m_oc²). Вычислить длину волны де Бройля для такого электрона.

239. На грань некоторого кристалла под углом a = 60^o к её поверхности падает параллельный пучок электронов, движущихся с одинаковой скоростью. Определить скорость v электронов, если они испытывают интерференционное отражение первого порядка. Расстояние d между атомными плоскостями кристалла равно 0, 2 нм.

240. Узкий пучок электронов, прошедших ускоряющую разность потенциалов U = 30 кВ, падает нормально на тонкий листок золота, проходит через него и рассеивается. На фотопластинке, расположенной за листком на расстоянии L = 20 см от него, получена дифракционная картина, состоящая из круглого центрального пятна и ряда концентрических окружностей. Радиус первой окружности r = 3,4 мм. Определить длину волны де Бройля электронов.

241. Параллельный пучок электронов, движущихся с одинаковой скоростью v= 1 Мм/с, падает нормально на диафрагму с длинной щелью шириной l = 1 мкм. Проходя через щель, электроны рассеиваются и образуют дифракционную картину на экране, расположенном на расстоянии d = 50 см от щели и параллельном плоскости диафрагмы. Определить линейное расстояние x между первыми дифракционными минимумами.

242. С какой скоростью движется электрон, если длина волны де Бройля электрона равна его комптоновской длине волны.

243. Электрон движется по окружности радиусом r = 0,5 см в однородном магнитном поле с индукцией B = 8 мТл. Определить длину волны де Бройля электрона.

244. Какую ускоряющую разность потенциалов должен пройти электрон, чтобы длина волны де Бройля была равна 1 пм?

245. Протон обладает кинетической энергией T = 1 кэВ. Определить дополнительную энергию DT, которую необходимо ему сообщить, для того, чтобы длина волны де Бройля уменьшилась в три раза.

246. Узкий пучок моноэнергетических электронов с кинетической энергией T= = 10 мэВ проходит через поликристаллическую алюминиевую фольгу, образуя на экране систему дифракционных колец. Вычислить межплоскостное расстояние, соответствующее отражению третьего порядка от некоторой системы кристаллических плоскостей, если ему отвечает дифракционное кольцо диаметра D = 3,20 см. Расстояние между экраном и фольгой L = 10,0 см.

247. Узкий пучок моноэнергетических электронов падает нормально на поверхность монокристалла никеля. В направлении, составляющем угол q = 55⁰ с нормалью к поверхности, наблюдается максимум отражения четвёртого порядка при энергии электронов T =180 эВ. Вычислить соответствующее значение межплоскостного расстояния.

248. Вычислить дебройлевские длины волн электрона и атома урана, имеющих одинаковую кинетическую энергию 100 эВ.

249. Вычислить дебройлевскую длину волны релятивистского электрона, движущегося с кинетической энергией T = 0,3 МэВ.

250. Нейтрон с кинетической энергией T =25 эВ налетает на покоящийся дейтрон ( ядро тяжёлого водорода). Найти дебройлевские длины волн обеих частиц в системе их центра инерции.

251. Определить неточность Dx в определении координаты электрона, движущегося в атоме водорода со скоростью v = 1.5×10⁶ м/с, если допускаемая неточность Dv в определении скорости составляет 10% от её величины. Сравнить полученную неточность с диаметром d атома водорода , вычисленным по теории Бора для основного состояния , и указать, применимо ли понятие траектории в данном случае.

252. Электрон с кинетической энергией T =1 эВ находится в металлической пылинке диаметром d =1 мкм. Определить относительную неточность Dv, с которой может быть определена скорость электрона.

253. Во сколько раз дебройлевская длина волны l частицы меньше не-определённости Dx её координаты, которая соответствует относительной неопределённости импульса в 1% ?

254. Предполагая , что неопределённость координаты движущейся частицы равна дебройлевской длине волны, определить относительную неточность Dp/p импульса этой частицы.

255. Используя соотношение неопределённостей, оценить ширину l одно-мерного потенциального ящика, в котором минимальная энергия электрона E_min = 10 эВ.

256. Используя соотношение неопределённостей, оценить низший энергети-ческий уровень электрона в атоме водорода. Принять линейные размеры атома d = 0,1 нм.

257. Приняв, что минимальная энергия E нуклона в ядре равна 10 МэВ, оценить, из соотношения неопределённостей, линейные размеры ядра.

258. Показать, используя соотношение неопределённостей, что в ядре не могут находится электроны. Линейные размеры ядра принять равными 5 фм.

259. Рассмотрим следующий мысленный эксперимент. Пусть моноэнерге-тический пучок электронов (Т=10 эВ) падает на щель шириной a. Можно сказать, что если электрон прошёл через щель, то его координата известна с неточностью Dx=a. Оценить полученную при этом относительную не-точность в определении импульса Dp/p электрона в случае, если а=0.1 нм.

260. Пылинки массой m = 10^-12 г взвешены в воздухе и находятся в тепловом равновесии. Можно ли установить, наблюдая за движением пылинок, отклонение от законов классической механики? Принять, что воздух находится при нормальных условиях, пылинки имеют сферическую форму. Плотность вещества, из которого состоят пылинки, равна 2×10³ кг/м³.

261. Используя соотношение неопределённостей DE×Dt ³ ħ, оценить ширину Г энергетического уровня в атоме водорода , находящегося : 1) в основном состоянии ; 2) в возбуждённом состоянии, время t жизни атома в возбуждённом состоянии равно 10^-8 с.

262. Оценить относительную ширину Dw/w спектральной линии, если известны время жизни атома в возбуждённом состоянии t ~10^-8 c и длина волны излучаемого фотона (l = 0,6 мкм ).

263. Какова должна быть кинетическая энергия протона в моноэнергетическом пучке, используемом для исследования структуры с линейными размерами l ~ 10^-13 см.

264. Для приближенной оценки минимальной энергии электрона в атоме водорода можно предположить, что неопределённость Dr радиуса r электронной орбиты и неопределённость Dp импульса p электрона на такой орбите соответственно связаны следующим образом: Dr ~ r и Dp ~ p. Используя эти связи, а также соотношение неопределённостей, определить минимальное значение энергии T_min электрона в атоме водорода.

265. Среднее время жизни Dt атома в возбуждённом состоянии составляет около 10^-8 с. При переходе атома в нормальное состояние испускается фотон, средняя длина волны, которого равна 400 нм. Оценить относительную ширину Dl/l излучаемой спектральной линии, если не происходит уширения линии за счёт других процессов.

266. Электрон с кинетической энергией T ~ 4 МэВ локализован в области размером l = 1 мкм. Оценить с помощью соотношения неопределённостей относительную неопределённость его скорости.

267. Электрон находится в одномерной прямоугольной потенциальной яме с бесконечно высокими стенками. Ширина ямы равна l=0,1 нм. Оценить с помощью соотношения неопределённостей силу давления электрона на стенки этой ямы при минимально возможной энергии.

268. Используя соотношение неопределённостей, оценить наименьшие ошибки Dv в определении скорости электрона и протона, если координаты центра масс этих частиц могут быть установлены с неопределённостью 1 мкм.

269. Альфа-частица находится в бесконечно глубоком, одномерном, прямоугольном потенциальном ящике. Используя соотношение неопределённостей, оценить ширину l ящика, если известно, что минимальная энергия a - частицы E_min = 8 МэВ.

270. Принимая, что электрон находится внутри атома диаметром 0,3 нм, определить неопределённость энергии этого электрона.

271. Электронный пучок выходит из электронной пушки под действием разности потенциалов U = 200 В. Определить, можно ли одновременно измерить траекторию электрона с точностью до 100 пм и его скорость с точностью до 10%.

272. Оценить с помощью соотношения неопределённостей минимальную кинетическую энергию электрона, движущегося внутри сферы радиусом R = 0,05 нм.

273. Электронный пучок ускоряется в электронно-лучевой трубке разностью потенциалов U = 1 кВ. Известно, что неопределённость скорости составляет 0,1% от её числового значения. Определить неопределённость координаты электрона. Являются ли электроны в данных условиях квантовыми или классическими частицами?

274. Частица массы m = 9,1×10^-31 кг движется в одномерном потенциальном поле U = k×x²/2 (гармонический осциллятор). Оценить с помощью соотношения неопределённостей минимально возможную энергию частицы в таком поле, если k = 1,12 Н/м.

275. Оценить с помощью соотношения неопределённостей минимально возможную энергию электрона в атоме водорода и соответствующее эффективное расстояние его от ядра.

276. Частица находится в потенциальном ящике. Найти отношение разности соседних энергетических уровней DE_n+1,n к энергии Е_n частицы в двух случаях: 1) n=3; 2) n®µ . Результаты пояснить рисунком.

277. Электрон находится в потенциальном ящике шириной l=0,5 нм. Опре-делить наименьшую разность DЕ энергетических уровней электрона. Ответ выразить в электрон-вольтах.

278. Частица в потенциальном ящике находится в основном состоянии. Какова вероятность W нахождения частицы: 1) в средней трети ящика; 2) в крайней трети ящика?

279. В одномерном потенциальном ящике шириной l находится электрон. Вычислить вероятность w нахождения электрона на первом энергетическом уровне в интервале 1/4, равноудаленном от стенок ящика.

280. Вычислить отношение вероятности w₁/w₂ нахождения электрона на первом и втором энергетических уровнях в интервале 1/4, равноудаленном от стенок одномерной потенциальной ямы шириной l.

281. Электрон находится в одномерном потенциальном ящике шириной l. Определить среднее значение координаты <x> электрона внутри ящика.

282. Волновая функция, описывающая движение электрона в основном состоянии атома водорода, имеет вид 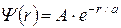, где a = 0,53×10^-10 м - радиус первой боровской орбиты, A - постоянная нормировки. Найти для основного состояния атома водорода наиболее вероятное расстояние электрона от ядра.

283. Собственная функция, описывающая основное состояние электрона в атоме водорода, имеет вид , где a - радиус первой боровской орбиты. Найти среднее расстояние электрона от ядра.

284. Электрон находится в бесконечно глубоком, одномерном, прямоугольном потенциальном ящике шириной l. В каких точках в интервале 0 < x < l плотности вероятности нахождения электрона на втором и третьем энергетических уровнях одинаковы? Вычислить плотность вероятности для этих точек. Решение пояснить графиком.

285. Частица в потенциальном ящике шириной l находится в возбуждённом состоянии (n =2). Определить, в каких точках интервала 0 < x < l плотность вероятности нахождения частицы:1) максимальна; 2) минимальна.

286. Найти вероятность W прохождения электрона через прямоугольный потенциальный барьер при разности энергий U-E=1 эВ, если ширина барьера: 1) d=0,1 нм; 2) d=0,5 нм.

287. Электрон проходит через прямоугольный потенциальный барьер шириной d=0,5 нм. Высота U барьера больше энергии Е электрона на 1%. Вычислить коэффициент прозрачности D, если энергия электрона Е=10 эВ.

288. Ширина d прямоугольного потенциального барьера равна 0,2 нм. Разность энергий U-E=1 эВ. Во сколько раз изменится вероятность W прохождения электрона через барьер, если разность энергий возрастет в n=10 раз?

289. При какой ширине d прямоугольного потенциального барьера коэффициент прозрачности D для электронов равен 0,01? Разность энергий U-E=10 эВ.

290. Электрон с энергией Е движется в положительном направлении оси Х. При каком значении U-Е, выраженном в электрон-вольтах, коэффициент прозрачности D=10^-3, если ширина d барьера равна 0,1 нм?

291. Электрон с энергией Е=9 эВ движется в положительном направлении оси Х. Оценить вероятность W того, что электрон пройдет через потенциальный барьер, если его высота U=10 эВ и ширина d=0,1 нм.

292. Прямоугольный потенциальный барьер имеет ширину d=0,1 нм. При какой разности энергий U-Е вероятность W прохождения электронов через барьер равна 0,99?

293. Ядро испускает a-частицы с энергией Е=5 МэВ. В грубом приближении можно считать, что a-частицы проходят через прямоугольный потенциальный барьер высотой U=10 МэВ и шириной d=5 фм. Найти коэффициент прозрачности D барьера для a-частиц.

294. Волновая функция, описывающая движение электрона в основном состоянии атома водорода, имеет вид 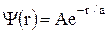, где a - радиус первой боровской орбиты. Найти для основного состояния атома водорода среднее значение <F> кулоновской силы.

295. Собственная волновая функция, описывающая основное состояние электрона в атоме водорода, имеет вид 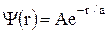, где A - постоянная нормировки, a - первый боровский радиус. Найти среднее значение потенциальной энергии электрона в атоме водорода.

296. Атом водорода находится в основном состоянии. Собственная волновая функция, описывающая основное состояние в атоме, имеет вид 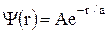, где A - некоторая константа. Найти из условия нормировки постоянную A.

297. Атом водорода находится в основном состоянии. Вычислить вероятность того, что электрон находится внутри области, ограниченной сферой, радиуса, равного радиусу первой боровской орбиты.

298. Волновая функция, описывающая 2s - состояние электрона в атоме водорода, имеет вид , где r = r/a, a -первый боровский радиус; C = . Определить расстояние от ядра, на котором вероятность обнаружить электрон имеет максимум.

299. Частица находится в основном состоянии в прямоугольной потенциальной яме шириной l с абсолютно непроницаемыми стенками. Во сколько раз отличаются вероятности местонахождения частицы в крайней трети и крайней четверти ямы?

300. Волновая функция частицы массы m = 9,1×10^-31 кг для основного состояния в одномерном потенциальном поле U(x) = kx²/2 имеет вид y(x)=Aexp(-ax²), где A - нормировочный коэффициент, a- положительная постоянная, k = 0,91 Н/м. Найти с помощью уравнения Шрёдингера постоянную a и энергию частицы в этом состоянии.

301. Зная постоянную Авогадро N_a, определить массу m, нейтрального атома углерода C¹² и массу m, соответствующую углеродной единице массы.

302. Хлор представляет собой смесь двух изотопов с относительными атомными массами А₁ = 34,969 и А₂ = 36,966. Вычислить относительную атомную массу А хлора, если массовые доли w₁ и w₂ первого и второго изотопов соответственно равны 0,754 и 0,246.

303. Какую часть массы нейтрального атома плутония составляет масса его электронной оболочки?

304. Определить концентрацию нуклонов в ядре.

305. Оценить, какую часть от объема атома кобальта составляет объем его ядра. Плотность r кобальта равна 4,5×10³ кг/м³.

306. Показать, что средняя плотность <r> ядерного вещества одинакова для всех ядер. Оценить (по порядку величины) ее значение.

307. Два ядра сблизились до расстояния, равного диаметру ядра. Считая, что масса и заряд равномерно распределены по объему ядра, определить силу F₁ гравитационного притяжения, силу F₂ кулоновского отталкивания и отношение этих сил (F₁/F₂).

308. Покоившееся ядро радона 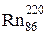выбросило a- частицу со скоростью V=16 Мм/с. В какое ядро превратилось ядро радона? Какую скорость V₁ получило оно в результате отдачи?

309. Какова вероятность W того, что данный атом в изотопе радиоактивного йода I¹³¹ распадается в течение ближайшей секунды?

310. Какая часть начального количества атомов распадется за один год в радиоактивном изотопе тория Th²²⁸?

311. При распаде радиоактивного полония Ро²¹⁰ в течение времени t=1 ч образовался гелий 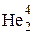, который при нормальных условиях занял объем V=89,5 см³. Определить период полураспада полония.

312. Период полураспада T_1/2 радиоактивного нуклида равен 1 ч. Определить среднюю продолжительность жизни этого нуклида.

313. Определить число N атомов, распадающихся в радиоактивном изотопе за время t=10 с, если его активность А=0,1 МБк. Считать активность постоянной в течение указанного времени.

314. Активность А препарата уменьшилась в n=250 раз. Скольким периодам полураспада равен протекший промежуток времени t?

315. За время t=1 сут активность изотопа уменьшилась от А₁=118 ГБк до А₂=7,4 ГБк. Определить период полураспада этого нуклида.

316. Счетчик Гейгера, установленный вблизи препарата радиоактивного изотопа серебра, регистрирует поток b - частиц. При первом измерении поток Ф₁ b -частиц был равен 87 с^-1, а по истечении времени t=1 сут поток Ф₂ оказался равным 22 с^-1. Определить период полураспада T_1/2 изотопа.

317. Определить активность А фосфора Р³² массой m= 1 мг.

318. Вычислить удельную активность а кобальта Co⁶⁰.

319. Найти отношение массовой активности а₁ стронция к массовой актив-ности а₂ радия Ra²²⁶.

320. Найти массу m₁ урана U²³⁸, имеющего такую же активность А, как стронций Sr⁹⁰ массой m₂ = 1 мг.

321. Определить массу m₂ радона Rn²²², находящегося в радиоактивном равновесии с радием Ra²²⁶ массой m₁=1 г.

322. Уран U²³⁴ является продуктом распада наиболее распространенного изотопа урана U²³⁸. Определить период полураспада T_1/2 урана U²³⁴ , если его массовая доля w в естественном уране U²³⁸ равна 6×10^-5.

323. Точечный изотропный радиоактивный источник создает на расстоянии r=1 м интенсивность I g-излучения, равную 1,6 мВт/м². Принимая, что при каждом акте распада ядра излучается один g-фотон с энергией e =1,33 МэВ, определить активность А источника.

324. Определить интенсивность I гамма-излучения на расстоянии r=5 см от точечного изотропного радиоактивного источника имеющего активность А=148 ГБк. Считать, что при каждом акте распада излучается, в среднем, n= 1,8 g -фотонов с энергией e = 0,51 МэВ каждый.

325. Определить возраст древних деревянных предметов, если известно, что удельная активность изотопа C¹⁴ у них составляет 3/5 удельной активности этого же изотопа в только что срубленных деревьях. Период полураспада ядер C¹⁴ равен 5570 лет.

326. Радиоактивный изотоп Na²² излучает g -кванты энергии e = 1,28 МэВ. Определить мощность Р гамма-излучения и энергию W, излучаемую за время t=5 мин изотопом натрия массой m =5 г. Считать, что при каждом акте распада излучается один g - фотон с указанной энергией.

327. Определить дефект массы Dm и энергию связи E_св ядра атома тяжёлого водорода.

328. Определить энергию E_св, которая освободится при соединении одного протона и двух нейтронов в атомное ядро.

329. Определить удельную энергию связи E_уд ядра .

330. Энергия связи Е_св ядра , состоящего из двух протонов и одного нейтрона, равна 7,72 МэВ. Определить массу m_a нейтрального атома, имеющего это ядро.

331. Определить массу m_a нейтрального атома, если ядро этого атома состоит из трёх протонов и двух нейтронов и энергия связи Е_св ядра 26,3 МэВ.

332. Атомное ядро, поглотившее g-фотон (e = 0,47 пм), пришло в возбуж-дённое состояние и распалось на отдельные нуклоны, разлетевшиеся в разные стороны. Суммарная кинетическая энергия Т нуклонов равна 0,4 МэВ . Определить энергию связи Е_св ядра.

333. Какую наименьшую энергию Е_св нужно затратить , чтобы разделить на отдельные нуклоны ядра 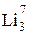и ? Почему для ядра бериллия эта энергия меньше, чем для ядра лития?

334. Определить энергию связи Есв , которая выделится при образовании из протонов и нейтронов ядер гелия 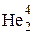массой m = 1 г.

335. Фотон с энергией e =3 МэВ, в поле тяжёлого ядра превратился в пару электрон - позитрон. Принимая, что кинетическая энергия частиц одинакова, определить кинетическую энергию Т каждой частицы.

336. Пренебрегая кинетическими энергиями ядер дейтерия и принимая их суммарный импульс равным нулю, определить кинетические энергии Т₁ и Т₂ и импульсы p1 и p₂ продуктов реакции

.

337. При делении одного ядра урана-235 выделяется энергия Q = 200 МэВ. Какую долю энергии покоя ядра урана-235 составляет выделившаяся энергия?

338. Определить энергию Е , которая освободится при делении всех ядер, содержащихся в уране-235 массой m =1 г.

339. Найти отношение скорости v₂ нейтрона после столкновения его с ядром углерода С¹² к начальной скорости v₁ нейтрона. Найти такое же отношение кинетических энергий нейтрона. Считать ядро углерода до столкновения покоящимся, столкновение прямым, центральным, упругим.

340. Ядро урана , захватив один нейтрон, разделилось на два осколка, причём освободилось два нейтрона. Одним из осколков оказалось ядро ксенона . Определить порядковый номер Z и массовое число А второго осколка.

341. Определить массовый расход m₁ ядерного горючего U²³⁵ в ядерном реакторе атомной электростанции. Тепловая мощность Р электростанции равна 10 МВт. Принять энергию Q, выделяющуюся при одном акте деления, равной 200 МэВ. К.п.д. электростанции составляет 20%.

342. Найти электрическую мощность Р атомной электростанции, расхо-дующей 0,1 кг урана - 235 в сутки, если к.п.д. станции равен 16%.

343. При соударении g-фотона с дейтоном последний может расщепиться на два нуклона. Написать уравнение ядерной реакции и определить минимальную энергию g-фотона, способного вызывать такое расщепление.

344. Неподвижное ядро кремния 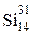выбросило отрицательно заряженную b-частицу с кинетической энергией Т = 0,5 МэВ. Пренебрегая кинетической энергией ядра отдачи, определить кинетическую энергию Т₁ антинейтрино.

345. Определить скорости продуктов реакции B¹⁰ (p, n) Li⁷, протекающей в результате взаимодействия тепловых нейтронов с покоящимися ядрами бора.

346. Свободный нейтрон радиоактивен. Выбрасывая электрон и антинейтрино, он превращается в протон. Определить суммарную кинетическую энергию Т всех частиц, возникающих в процессе превращения нейтрона. Принять, что кинетическая энергия нейтрона равна нулю и что масса покоя антинейтрино пренебрежимо мала.

347. Покоившееся ядро полония выбросило a-частицу с кинетической энергией Т = 5,3 МэВ. Определить кинетическую энергию Т ядра отдачи и полную энергию Q, выделившуюся при a-распаде.

348. Нейтральный p-мезон (p_o), распадаясь, превращается в два одинаковых g- фотона. Определить энергию e фотона. Кинетической энергией и импульсом мезона пренебречь.

349. Электрон и позитрон, имевшие одинаковые кинетические энергии, равные 0,24 МэВ, при соударении превратились в два одинаковых фотона. Определить энергию e фотона и соответствующую ему длину волны l.

350. Найти энергию Q ядерной реакции N (n, p)С¹⁴, если энергия связи E_св ядра N¹⁴ равна 104,66 МэВ, а ядра С¹⁴ - 105,29 МэВ.

351. Определить теплоту Q, необходимую для нагревания кристалла калия массой m = 200 г от температуры T₁ = 4 K до температуры T₂ = 5 K. Принять характеристическую температуру Дебая для калия q_D = 100 K и считать условие T < q_D выполненным.

352. Вычислить по классической теории теплоёмкости теплоёмкость C бромида алюминия AlBr₃ объёмом V = 1 м³. Плотность r кристалла бромида алюминия равна 3,01×10³ кг/м³.

353. Определить энергию U системы, состоящей из N=10²⁵ квантовых трёх-мерных независимых осцилляторов, при температуре T=q_E (q_E=300 K).

354. Медный образец массой m = 100 г находится при температуре T₁= 10 K. Определить теплоту Q, необходимую для нагревания образца до температуры T₂ = 20 K. Характеристическую температуру Дебая для меди принять равной 300 K, а условие T < q_D считать выполненным.

355. Зная, что для алмаза q_D = 2000 K, вычислить его удельную теплоёмкость при температуре T = 30 K.

356. Используя квантовую теорию теплоёмкости Эйнштейна, определить коэффициент упругости b связи атома в кристалле алюминия. Принять для алюминия q_E = 300 K.

357. Вычислить по теории Эйнштейна молярную нулевую энергию U_mo кристалла цинка. Характеристическая температура q_E для цинка равна 230 K.

358. Вычислить молярную внутреннюю энергию U_m кристаллов с двумерной решёткой, если характеристическая температура Дебая равна 350 K.

359. Найти отношение средней энергии <e_кв> линейного одномерного осциллятора, вычисленной по квантовой теории, к энергии <e_кл> такого же осциллятора, вычисленной для двух температур:1) T = 0,1q_E; 2) T = q_E.

360. Найти отношение изменения DU внутренней энергии кристалла при нагревании его от нуля до T = 0,1 q_D к нулевой энергии U_om. Считать T < q_D.

361. Определить относительную погрешность, которая будет допущена при вычислении теплоёмкости кристалла, если вместо значения, даваемого теорией Дебая (при Т = q_D), воспользоваться значением, даваемым законом Дюлонга-Пти.

362. Найти отношение D_E/D_D характеристических температур Эйнштейна и Дебая.

363. Найти энергию e фонона, соответствующего максимальной частоте w = 0,1 w_max Дебая, если характеристическая температура Дебая равна 250 K.

364. Молярная теплоёмкость серебра при температуре T = 20 K оказалась равной 1,65 Дж/(моль×K). Вычислить по значению теплоёмкости харак-теристическую температуру q_D. Условие T < q_D считать выполненным.

365. Определить квазиимпульс p фонона, соответствующего частоте w = 0,1w_max. Усреднённая скорость v звука в кристалле равна 1380 м/с, характеристическая температура Дебая равна 100 K. Дисперсией звуковых волн в кристалле пренебречь.

366. Определить усреднённую скорость звука в кристалле, характеристическая температура которого равна 300 K. Межатомное расстояние в кристалле равно 0,25 нм.

367. Длина волны l фонона, соответствующего частоте w = 0,01w_max, равна 52 нм. Пренебрегая дисперсией звуковых волн, определить характеристическую температуру q_D Дебая, если усреднённая скорость звука в кристалле равна 4,8 км/с.

368. Вычислить молярную нулевую энергию U_mo кристалла с одномерной решёткой, если характеристическая температура q_D Дебая равна 300 K.

369. Пользуясь теорией теплоёмкости Эйнштейна, определить изменение DU_m молярной внутренней энергии кристалла при нагревании его от нуля до T₁ = 0,1 q_E. Характеристическую температуру q_E Эйнштейна принять равной 300 K.

370. Вычислить энергию нулевых колебаний, приходящуюся на один грамм меди, дебаевская температура которой q_D = 330 K.

371. Определить максимальную частоту w_max собственных колебаний в кристалле золота по теории Дебая. Характеристическая температура q_D равна 180 K.

372. Характеристическая температура q_D Дебая для вольфрама равна 310 K. Определить длину волны l фононов, соответствующих частоте w = 0,1w_max. Усреднённую скорость звука в вольфраме вычислить. Дисперсией волн в кристалле пренебречь.

373. Вычислить максимальную частоту w_max Дебая для серебра, если известно, что молярная теплоёмкость C_m при T = 20 K равна 1,7 Дж/(моль×К).

374. Во сколько раз изменится средняя энергия <e> квантового осциллятора, приходящаяся на одну степень свободы, при повышении температуры от T₁ = q_E/2 до T₂ = q_E? Учесть нулевую энергию.

375. Определить отношение 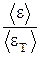средней энергии квантового осциллятора к средней энергии теплового движения молекул идеального газа при температуре T = q_E.

376. Определить долю свободных электронов в металле при T=0 K, энергии e которых заключены в интервале значений от 0,5e_max до e_max.

377. Германиевый кристалл, ширина DE запрещённой зоны в котором равна 0,72 эВ, нагревают от температуры t₁= 0^oС до температуры t₂ = 10^oC. Во сколько раз возрастёт его удельная проводимость?

378. При нагревании кремниевого кристалла от температуры t₁= 0^oC до температуры t₂ = 10^oC его удельная проводимость возрастает в 2,28 раза. По приведённым данным определить ширину DE запрещённой зоны кристалла кремния.

379. Сопротивление R₁ кристалла PbS при температуре t₁ = 20^oC равно 10⁴ Ом. Определить его сопротивление R₂ при температуре t₂ равной 80^oC.

380. Прямое напряжение U, приложенное к p-n переходу, равно 2 В. Во сколько раз возрастёт сила тока через переход, если изменить температуру от T₁ = 300 K до T₂ = 273 K?

381. Металл находится при температуре 0 K. Определить относительное число электронов, энергия которых отличается от энергии Ферми не более чем на 2%.

382. Вычислить среднюю кинетическую энергию электронов в металле при температуре T = 0 K, если уровень Ферми e_f = 7 эВ.

383. Определить вероятность того, что электрон в металле займёт энергетическое состояние, находящееся в интервале De =0,05 эВ ниже уровня Ферми и выше уровня Ферми для температуры 250 K.

384. Металл находится при температуре T = 0 K. Определить во сколько раз число электронов со скоростями от 0,5v_max до v_max больше числа электронов со скоростями от 0 до 0,5v_max.

385. Определить число свободных электронов, которое приходится на один атом натрия при температуре T = 0 K. Уровень Ферми e_f для натрия равен 3,12 эВ. Плотность r натрия равна 970 кг/м³.

386. Оценить температуру вырождения для калия, если принять, что на каждый атом приходится по одному свободному электрону. Плотность r калия равна 860 кг/м³.

387. Определить максимальную скорость электронов в металле при T = 0 K, если уровень Ферми e_f = 5 эВ.

388. Вычислить среднюю скорость электронов для металла, уровень Ферми которого при T = 0 K равен 6 эВ.

389. Определить отношение концентраций n₁/n₂ свободных электронов при T = 0 K в литии и цезии, если известно, что уровни Ферми в этих металлах соответственно равны e_f,1 = 4,72 эВ, e_f,2= 1,53 эВ.

390. Определить концентрацию свободных электронов в металле при температуре T = 0 K. Энергию Ферми принять равной 1 эВ.

391. Металлы литий и цинк приводят в соприкосновение друг с другом при температуре T = 0 K. На сколько изменится концентрация электронов проводимости в цинке? Какой из этих металлов будет иметь более высокий потенциал?

392. Каково значение энергии Ферми у электронов проводимости двухвалентной меди?

393. Германиевый образец нагревают от 0 до 17^oC. Принимая ширину запрещённой зоны германия DE = 0,72 эВ, определить, во сколько раз возрастёт его удельная проводимость.

394. Найти минимальную энергию, необходимую для образования пары электрон-дырка в кристалле CaAs, если его удельная проводимость изменяется в 10 раз при изменении температуры от 20 до 3^oC.

395. P-n переход находится под обратным напряжением U = 0,1 В. Его сопротивление R₁ = 692 Ом. Каково сопротивление R₂ перехода при прямом напряжении?

396. Сопротивление R₁ p-n перехода, находящегося под прямым напряжением U = 1 В, равно 10 Ом. определить сопротивление R₂ перехода при обратном напряжении.

397. Определить угловую скорость вращения молекулы S₂, находящейся на первом возбуждённом вращательном уровне, если расстояние между её ядрами d = 180 пм.

398. Найти механический момент молекулы кислорода, вращательная энергия которой E = 2,16 МэВ, а расстояние между ядрами d = 121 пм.

399. Вычислить длины волн красного и фиолетового спутников, ближайших к несмещённой линии, в колебательном спектре комбинационного рассеяния молекул F₂, если длина волны падающего света l = 404,7 нм и собственная частота колебаний молекулы w-= 2,15×10¹⁴ рад/с.

400. Вычислить дебаевскую температуру для железа, у которого скорости распространения продольных и поперечных колебаний равны соответственно 5,85 и 3,23 км/с.